No CrossRef data available.
Article contents
On dual unit balls of Thurston norms
Published online by Cambridge University Press: 07 October 2021
Abstract
Thurston norms are invariants of 3-manifolds defined on their second homology and understanding the shape of their dual unit balls is a widely open problem. In this article, we provide a large family of polytopes in 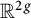 $\mathbb {R}^{2g}$
that appear like dual unit balls of Thurston norms, generalizing Thurston’s construction for polygons in
$\mathbb {R}^{2g}$
that appear like dual unit balls of Thurston norms, generalizing Thurston’s construction for polygons in 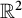 $\mathbb {R}^2$
.
$\mathbb {R}^2$
.
À mes enseignants, premiers
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021
References
Agol, I., Hass, J., and Thurston, W., The computational complexity of knot genus and spanning area. Trans. AMS 358(2006), no. 9, 3821–3850.10.1090/S0002-9947-05-03919-XCrossRefGoogle Scholar
Cossarini, M. and Dehornoy, P., Intersection norms on surfaces and Birkhoff sections for geodesic flows. Preprint, 2021. arXiv:1604.06688
Google Scholar
Gabai, D., Foliations and the topology of 3-manifolds. J. Differ. Geom. 18(1983), 445–503.10.4310/jdg/1214437784CrossRefGoogle Scholar
Hatcher, A., Notes on basic 3-manifold topology. http://pi.math.cornell.edu/hatcher/3M/3Mfds.pdf
Google Scholar
Lackenby, M., The efficient certification of knottedness and Thurston norm. Adv. Math. (accepted) arXiv:1604.00290
Google Scholar
Montesinos, J. M., Classical tessellations and three-manifolds. Springer-Verlag, Berlin.CrossRefGoogle Scholar
Sane, A., Intersection norm and one-faced collections. Comp. Rendus Math. 358, no. 8 (2020), 941–956.Google Scholar
Scharlemann, M., Sutured manifolds and generalized Thurston norms. J. Differ. Geom. 29(1989), 557–614.10.4310/jdg/1214443063CrossRefGoogle Scholar
Thurston, W., A norm for the homology of three manifolds. Mem. Amer. Math. Soc. 339(1986), 99–130.Google Scholar
Turaev, V., A norm for the cohomology of 2-complexes. Alg. Geom. Top. 2(2002), 137–155.10.2140/agt.2002.2.137CrossRefGoogle Scholar
Waldhausen, F., Eine Klasse von 3-dimensionaler Mannigfaltigkeiten I. Inventiones 3(1967), 308–333.10.1007/BF01402956CrossRefGoogle Scholar



