Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T04:22:04.953Z Has data issue: false hasContentIssue false
  • English
  • Français

On Density Conditions for Interpolation in the Ball

Published online by Cambridge University Press:  20 November 2018

Nicolas Marco  and
Xavier Massaneda
Nicolas Marco
Affiliation:
Departament de Matemàtiques Universitat Autònoma de Barcelona 08193 Bellaterra Spain, e-mail: [email protected]
Xavier Massaneda
Affiliation:
Departament de Matemàtica Aplicada i Anàlisi Universitat de Barcelona Gran Via 585 08071 Barcelona Spain, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study interpolating sequences for two related spaces of holomorphic functions in the unit ball of 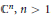${{\mathbb{C}}^{n}},\,n\,>\,1$. We first give density conditions for a sequence to be interpolating for the class 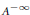${{A}^{-\infty }}$ of holomorphic functions with polynomial growth. The sufficient condition is formally identical to the characterizing condition in dimension 1, whereas the necessary one goes along the lines of the results given by Li and Taylor for some spaces of entire functions. In the second part of the paper we show that a density condition, which for 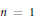$n\,=\,1$ coincides with the characterizing condition given by Seip, is sufficient for interpolation in the (weighted) Bergman space.

Keywords

32A3632A3830E05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 4 , 01 December 2003 , pp. 559 - 574
Copyright
Copyright © Canadian Mathematical Society 2003

References

[BC95] Berndtsson, B. and Ortega Cerdà, J., On interpolation and sampling in Hilbert spaces of analytic functions. J. Reine Angew.Math. 464 (1995), 109–128.Google Scholar
[BC00] Berndtsson, B. and Charpentier, P., A Sobolev mapping property of the Bergman kernel. Math. Z. (235) 1 (2000), 1–10.Google Scholar
[BGVY93] Berenstein, C. A., Gay, R., Vidras, A. and Yger, A., Residue currents and Bézout identities. Progr.Math. 114, Birkh¨auser Boston, 1993.Google Scholar
[BP89] Bruna, J. and Pascuas, D., Interpolation in A−∞ . J. London.Math. Soc. (1989), 452–466.Google Scholar
[Del98] Delin, H., Pointwise estimates for the weighted Bergman projection kernel in Cn, using a weighted L2 estimate for the ∂ equation. Ann. Inst. Fourier. (Grenoble) 48 (1998), 967–997.Google Scholar
[Gru77] Gruman, L., The area of analytic varieties in Cn. Math. Scand. 41 (1977), 365–397.Google Scholar
[Hör90] Hörmander, L., An introduction to complex analysis in several variables. third ed., North-Holland, Amsterdam, 1990.Google Scholar
[JMT96] Jevtić, M., Massaneda, X., and Thomas, P. J., Interpolating sequences for the weighted Bergman spaces of the ball. Michigan Math. J. 43 (1996), 495–517.Google Scholar
[Kor75] Korenblum, B., An extension of the Nevanlinna theory. Acta. Math. 135 (1975), 187–219.Google Scholar
[Kor77] Korenblum, B., A Beurling type theorem. Acta Math. 138 (1977), 265–293.Google Scholar
[LT96] Li, B. Q. and Taylor, B. A., On the Bézout problem and area of interpolating varieties in Cn. Amer. J. Math. 118 (1996), 989–1010.Google Scholar
[Mas97] Massaneda, X., Interpolation by holomorphic functions in the unit ball with polynomial growth. Ann. Fac. Sci. Toulouse Math. VI(1997), 277–296.Google Scholar
[Mas98] Massaneda, X., A−∞-interpolation in the ball, Proc. EdinburghMath. Soc. 41 (1998), 359–367.Google Scholar
[Mas99] Massaneda, X., Density conditions for interpolation in A−∞ . J. Analyse Math. 79 (1999), 299–314.Google Scholar
[Sei94] Seip, K., Beurling type density theorems in the unit disk, Invent.Math. 113 (1994), 21–29.Google Scholar