Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Utumi, Y.
1963.
On rings of which any one-sided quotient rings are two-sided.
Proceedings of the American Mathematical Society,
Vol. 14,
Issue. 1,
p.
141.
Utumi, Yuzo
1966.
On the Continuity and Self-Injectivity of a Complete Regular Ring.
Canadian Journal of Mathematics,
Vol. 18,
Issue. ,
p.
404.
Rangaswamy, K. M.
1970.
Representing Baer rings as endomorphism rings.
Mathematische Annalen,
Vol. 190,
Issue. 2,
p.
167.
Rangaswamy, K. M.
and
Vanaja, N.
1971.
A note on modules over regular rings.
Bulletin of the Australian Mathematical Society,
Vol. 4,
Issue. 1,
p.
57.
Jeremy, Louis
1974.
Modules Et Anneaux Quasi-Continus.
Canadian Mathematical Bulletin,
Vol. 17,
Issue. 2,
p.
217.
Goodearl, K.R.
1974.
Simple self-injective rings need not be artinian.
Communications in Algebra,
Vol. 2,
Issue. 1,
p.
83.
Evans, M. W.
1975.
Projectively torsion-free modules.
Journal of the Australian Mathematical Society,
Vol. 20,
Issue. 2,
p.
207.
Goodearl, K.R.
and
Handelman, D.
1975.
Simple self-injective rings.
Communications in Algebra,
Vol. 3,
Issue. 9,
p.
797.
Faith, Carl
1976.
Algebra II Ring Theory.
Vol. 191,
Issue. ,
p.
61.
Jain, S. K.
and
Mueller, Bruno
1981.
Semiperfect rings whose proper cyclic modules are continuous.
Archiv der Mathematik,
Vol. 37,
Issue. 1,
p.
140.
Faith, Carl
1985.
The maximal regular ideal of self-injective and continuous rings splits off.
Archiv der Mathematik,
Vol. 44,
Issue. 6,
p.
511.
Tariq Rizvi, S.
1988.
Commutative rings for which every continuous module is quasi-injective.
Archiv der Mathematik,
Vol. 50,
Issue. 5,
p.
435.
Tuganbaev, A. A.
1999.
Skew-injective modules.
Journal of Mathematical Sciences,
Vol. 95,
Issue. 4,
p.
2328.
Birkenmeier, Gary F.
Kim, Jin Yong
and
Park, Jae Keol
2001.
PRINCIPALLY QUASI-BAER RINGS.
Communications in Algebra,
Vol. 29,
Issue. 2,
p.
639.
Oshiro, Kiyoichi
2001.
International Symposium on Ring Theory.
p.
279.
FAITH, CARL
and
VAN HUYNH, DINH
2002.
WHEN SELF-INJECTIVE RINGS ARE QF: A REPORT ON A PROBLEM.
Journal of Algebra and Its Applications,
Vol. 01,
Issue. 01,
p.
75.
Hanada, Katutosi
Kuratomi, Yosuke
and
Oshiro, Kiyoichi
2002.
On Direct Sums of Extending Modules and Internal Exchange Property.
Journal of Algebra,
Vol. 250,
Issue. 1,
p.
115.
Amin, Ismail
Ibrahim, Yasser
and
Yousif, Mohamed
2015.
C3-Modules.
Algebra Colloquium,
Vol. 22,
Issue. 04,
p.
655.
Ding, Nanqing
Ibrahim, Yasser
Yousif, Mohamed
and
Zhou, Yiqiang
2017.
C4-Modules.
Communications in Algebra,
Vol. 45,
Issue. 4,
p.
1727.
Atani, Shahabaddin Ebrahimi
Khoramdel, Mehdi
and
Hesari, Saboura Dolati Pish
2019.
T-idempotent invariant modules.
Journal of Algebra and Its Applications,
Vol. 18,
Issue. 06,
p.
1950115.


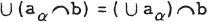 for every directed subset (a
for every directed subset (a