Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-22T20:44:38.402Z Has data issue: false hasContentIssue false
  • English
  • Français

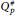On Classes for Hyperbolic Riemann Surfaces

Published online by Cambridge University Press:  20 November 2018

Rauno Aulaskari  and
Huaihui Chen
Rauno Aulaskari
Affiliation:
Department of Mathematics, University of Eastern Finland, P.O. Box 111, FIN-80101, Joensuu, Finland e-mail: [email protected]
Huaihui Chen
Affiliation:
Department of Mathematics, Nanjing Normal University, Nanjing 210097, P.R.China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

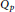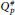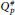The ${{Q}_{p}}$ spaces of holomorphic functions on the disk, hyperbolic Riemann surfaces or complex unit ball have been studied deeply. Meanwhile, there are a lot of papers devoted to the $Q_{p}^{\#}$ classes of meromorphic functions on the disk or hyperbolic Riemann surfaces. In this paper, we prove the nesting property (inclusion relations) of $Q_{p}^{\#}$ classes on hyperbolic Riemann surfaces. The same property for 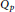${{Q}_{p}}$ spaces was also established systematically and precisely in earlier work by the authors of this paper.

Keywords

30D4530D5030F35Q# p classhyperbolic Riemann surfacespherical Dirichlet function
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 1 , 01 March 2016 , pp. 13 - 29
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Ahlfors, L., Conformai invariants, topics in geometric function theory. McGraw-Hill Series in Higher Mathematics, Mcgraw-Hill, New York, 1973.Google Scholar
[2] Anderson, J. M., Clunie, J., and Pommerenke, Ch., On Block functions and normal functions. J. Reine Angew. Math. 240(1974), 12–37.Google Scholar
[3] Aulaskari, R., On V MO A for Riemann surfaces. Canad. J. Math. 40(1988), no. 5,1174-1185. http://dx.doi.Org/10.4153/CJM-1988-049-9 Google Scholar
[4] Aulaskari, R. and Chen, H., Area inequality and Qp norm. J. Funct. Anal. 221(2005), no. 1,1-24. http://dx.doi.Org/10.1016/j.jfa.2004.12.007 Google Scholar
[5] Aulaskari, R., He, Y., Ristioja, J., and Zhao, R., Qp spaces on Riemann surfaces. Canad. J. Math. 50(1998), no. 3, 449–464. http://dx.doi.Org/10.4153/CJM-1998-024-4 Google Scholar
[6] Aulaskari, R. and Lappan, P., Criteria for an analytic function to be Block and a harmonic or meromorphic function to be normal. In: Complex analysis and its applications (Hong Kong, 1993), Pitman Res. Notes Math. Ser., 305, Longman Sci. Tech., Harlow, 1994, pp. 136–146.Google Scholar
[7] Aulaskari, R., Xiao, J., and Zhao, R., On subspaces and subsets ofBMOA and UBC. Analysis 15(1995), no. 2, 101–121.Google Scholar
[8] Dufresnoy, J., Sur l'aire sphérique décrite par les valeurs d'une fonction mefomorphe. Bull. Sci. Math. 65(1941), 214–219.Google Scholar
[9] Kobayashi, S., Image areas and BMO norms of analytic functions. Kodai Math. J. 8(1985), no. 2, 163–170. http://dx.doi.Org/10.2996/kmj71138037045 Google Scholar
[10] Kobayashi, S., Range sets and BMO norms of analytic functions. Canad. J. Math. 36(1984), no. 4, 747–755. http://dx.doi.Org/10.4153/CJM-1984-042-6 Google Scholar
[11] Lehto, O. and Virtanen, K. I., Boundary behaviour and normal meromorphic functions. Acta Math. 97(1957), 47–65. http://dx.doi.Org/10.1007/BF02392392 Google Scholar
[12] Ouyang, C., Yang, W., and Zhao, R., Mb'bius invariant Qp spaces associated with the Green's function on the unit ball o/C”. Pacific J. Math. 182(1998), no. 1, 69–99. http://dx.doi.Org/10.2140/pjm.1998.182.69 Google Scholar
[13] Xiao, J., Carleson measure, atomic decomposition and free interpolation from Bloch space. Ann. Acad. Sci. Fenn. Ser. AI Math. 19(1994), no. 1, 35–46.Google Scholar
[14] Xiao, J., Holomorphic Q classes. Lecture Notes in Mathematics, 1767, Springer-Verlag, Berlin, 2001.Google Scholar
[15] Yamashita, S., Functions of uniformly bounded characteristic. Ann. Acad. Sci. Fenn. Ser. A I Math. 7(1982), no. 2, 349–367. http://dx.doi.Org/10.5186/aasfm.1982.0733 Google Scholar
[16] Yamashita, S., Some unsolved problems on meromorphic functions of uniformly bounded characteristic. Internat. J. Math. Math. Sci. 8(1985), no. 3, 477–482. http://dx.doi.Org/!0.1155/SO161171285000527 Google Scholar