Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T18:48:11.977Z Has data issue: false hasContentIssue false
  • English
  • Français

On Certain Multivariable Subnormal Weighted Shifts and their Duals

Published online by Cambridge University Press:  20 November 2018

Ameer Athavale  and
Pramod Patil
Ameer Athavale
Affiliation:
Department of Mathematics, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India e-mail: [email protected]; [email protected]
Pramod Patil
Affiliation:
Department of Mathematics, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India e-mail: [email protected]; [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For every subnormal $m$-variable weighted shift $S$ (with bounded positive weights), there is a corresponding positive Reinhardt measure $\mu $ supported on a compact Reinhardt subset of ${{\mathbb{C}}^{m}}$. We show that, for 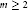$m\,\ge \,2$, the dimensions of the 1-st cohomology vector spaces associated with the Koszul complexes of $S$ and its dual 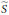$\widetilde{S}$ are different if a certain radial function happens to be integrable with respect to μ (which is indeed the case with many classical examples). In particular, $S$ cannot in that case be similar to 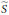$\widetilde{S}$. We next prove that, for 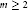$m\,\ge \,2$, a Fredholm subnormal $m$-variable weighted shift $S$ cannot be similar to its dual.

Keywords

47B20subnormalReinhardtBetti numbers
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 3 , 01 September 2013 , pp. 459 - 465
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Athavale, A., Model theory on the unit ball in Cm. J. Operator Theory 27 (1992, no. 2, 347–358.Google Scholar
[2] Athavale, A., Quasisimilarity-invariance of joint spectra for certain subnormal tuples. Bull. London Math. Soc. 40 (2008, no. 5, 759–769. http://dx.doi.org/10.1112/blms/bdn054 Google Scholar
[3] Athavale, A. and Patil, P., On the duals of Szegö and Cauchy tuples. Proc. Amer. Math. Soc. 139 (2011, no. 2, 491–498. http://dx.doi.org/10.1090/S0002-9939-2010-10482-3 Google Scholar
[4] Conway, J. B., The dual of a subnormal operator. J. Operator Theory 5 (1981, no. 2, 195–211.Google Scholar
[5] Curto, R. E., Fredholm and invertible n-tuples of operators. The deformation problem. Trans. Amer. Math. Soc. 266 (1981, no. 1, 129–159.Google Scholar
[6] Curto, R. E. and Salinas, N., Spectral properties of cyclic subnormal m-tuples. Amer. J. Math. 107 (1985, no. 1, 113–138. http://dx.doi.org/10.2307/2374459 Google Scholar
[7] Curto, R. E. and Yan, K., The spectral picture of Reinhardt measures. J. Func. Anal. 131 (1995, no. 2, 279–301. http://dx.doi.org/10.1006/jfan.1995.1090 Google Scholar
[8] Eschmeier, J., Grothendieck's comparison theorem and multivariable Fredholm theory. Arch. Math. 92 (2009, no. 5, 461–475.Google Scholar
[9] Gleason, J., On a question of Ameer Athavale. Irish Math. Soc. Bull. 48 (2002, 31–33.Google Scholar
[10] Gleason, J., Richter, S., and Sundberg, C., On the index of invariant subspaces in spaces of analytic functions in several complex variables. J. Reine Angew. Math. 587 (2005, 49–76. http://dx.doi.org/10.1515/crll.2005.2005.587.49 Google Scholar
[11] Itô, T., On the commutative family of subnormal operators. J. Fac. Sci. Hokkaido Univ. 14 (1958, 1-15.Google Scholar
[12] Jewell, N. and Lubin, A. R., Commuting weighted shifts and analytic function theory in several variables. J. Operator Theory 1 (1979, no. 2, 207–223.Google Scholar