Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T15:59:12.117Z Has data issue: false hasContentIssue false
  • English
  • Français

On Cauchy–Liouville–Mirimanoff Polynomials

Published online by Cambridge University Press:  20 November 2018

Pavlos Tzermias
Pavlos Tzermias*
Affiliation:
Department of Mathematics, University of Tennessee, Knoxville, TN 37996-1300, U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 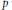$p$ be a prime greater than or equal to 17 and congruent to 2 modulo 3. We use results of Beukers and Helou on Cauchy–Liouville–Mirimanoff polynomials to show that the intersection of the Fermat curve of degree 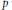$p$ with the line 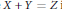$X+Y=Z$ in the projective plane contains no algebraic points of degree 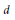$d$ with 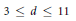$3\le d\le 11$. We prove a result on the roots of these polynomials and show that, experimentally, they seem to satisfy the conditions of a mild extension of an irreducibility theorem of Pólya and Szegö. These conditions are conjecturally also necessary for irreducibility.

Keywords

11G3011R0912D0512E10
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 2 , 01 June 2007 , pp. 313 - 320
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Beukers, F., On a sequence of polynomials. Algorithms for algebra. J. Pure Appl. Algebra 117/118(1997), 97–103.Google Scholar
[2] Bouniakowsky, V., Sur les diviseurs numériques invariables des fonctions rationelles entières. Mémoires Sci. Math. Phys. 6(1854-1855), 307–329.Google Scholar
[3] Brillhart, J., Filaseta, M. and Odlyzko, A., On an irreducibility theorem of A. Cohn. Canad. J. Math. 33(1981), no. 5, 1055–1059.Google Scholar
[4] Cauchy, A. and Liouville, J., Rapport sur un mémoire de M. Lamé relatif au dernier théoréme de Fermat. C. R. Acad. Sci. Paris 9(1839), 359–363.Google Scholar
[5] Debarre, O. and Klassen, M., Points of low degree on smooth plane curves. J. Reine Angew. Math. 446(1994), 81–87.Google Scholar
[6] Faddeev, D., The group of divisor class on some algebraic curves. Soviet Math. Dokl. 2(1961), 67–69.Google Scholar
[7] Gross, B. and Rohrlich, D., Some results on the Mordell-Weil group of the Jacobian of the Fermat curve. Invent. Math. 44(1978), no. 3, 201–224.Google Scholar
[8] Helou, C., On Wendt's determinant. Math. Comp. 66(1997) no. 219, 1341–1346.Google Scholar
[9] Helou, C., Cauchy-Mirimanoff polynomials. C. R. Math. Rep. Acad. Sci. Canada 19(1997), no. 2, 51–57.Google Scholar
[10] Klassen, M. and Tzermias, P., Algebraic points of low degree on the Fermat quintic. Acta Arith. 82(1997), no. 4, 393–401.Google Scholar
[11] McCallum, W., The arithmetic of Fermat curves. Math. Ann. 294(1992), no. 3, 503–511.Google Scholar
[12] McCallum, W. and Tzermias, P., On Shafarevich-Tate groups and the arithmetic of Fermat curves. In: Number Theory and Algebraic Geometry. London Math. Soc. Lecture Note Ser. 303, Cambridge University Press, Cambridge, 2003, pp. 203–226.Google Scholar
[13] Mirimanoff, D., Sur l’équatio (x + 1)l − xl − 1 = 0. Nouv. Ann. Math. 3(1903), 385–397.Google Scholar
[14] Ram Murty, M., Prime numbers and irreducible polynomials. Amer. Math. Monthly 109(2002), no. 5, 452–458.Google Scholar
[15] Pólya, G. and Szegö, G., Aufgaben und Lehrsätze aus der Analysis. Springer-Verlag, Berlin, 1964.Google Scholar
[16] Ribenboim, P., Homework!. In: Number Theory. CRM Proc. Lecture Notes 19, American Mathematical Socoety, Providence, RI, 1999, pp. 391–392.Google Scholar
[17] Ribenboim, P., 13 Lectures on Fermat's Last Theorem. Springer-Verlag, New York, 1979.Google Scholar
[18] Schinzel, A. and Sierpinski, W., Sur certaines hypothèses concernant les nombres premiers. Acta Arith. 4(1958), 185–208; Erratum, ibid. 5(1958) 259.Google Scholar
[19] Terjanian, G., Sur la loi de réciprocité des puissances l-émes. Acta Arith. 54(1989), no. 2, 87–125.Google Scholar
[20] Tzermias, P., Low-degree points on Hurwitz-Klein curves. Trans. Amer. Math. Soc. 356(2004), no. 3, 939–951.Google Scholar
[21] Tzermias, P., Parametrization of low-degree points on a Fermat curve. Acta Arith. 108(2003), no. 1, 25–35.Google Scholar
[22] Tzermias, P., Algebraic points of low degree on the Fermat curve of degree seven. Manuscripta Math. 97(1998), no. 4, 483–488.Google Scholar