Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T13:07:46.906Z Has data issue: false hasContentIssue false
  • English
  • Français

On Bodies Associated with a Given Convex Body

Published online by Cambridge University Press:  20 November 2018

Endre Makai Jr.  and
Horst Martini
Endre Makai Jr.
Affiliation:
Mathematical Institute of the Hungarian Academy of Sciences, Pf 127, H-l364 Budapest, HUNGARY, [email protected]
Horst Martini
Affiliation:
Fakultät für Mathematik Technische Universität Chemnitz-Zwickau, D-09107 Chemnitz, GERMANY, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let d ≥ 2, and K ⊂ ℝd be a convex body with 0 ∈ int K. We consider the intersection body IK, the cross-section body CK and the projection body ΠK of K, which satisfy IK ⊂ CK ⊂ ΠK. We prove that [bd(IK)] ∩ [bd(CK)] ≠ 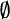(a joint observation with R. J. Gardner), while for d ≥ 3 the relation [CK] ⊂ int(ΠK) holds for K in a dense open set of convex bodies, in the Hausdorff metric. If IK = c ˙ CK for some constant c > 0, then K is centred, and if both IK and CK are centred balls, then K is a centred ball. If the chordal symmetral and the difference body of K are constant multiples of each other, then K is centred; if both are centred balls, then K is a centred ball. For d ≥ 3 we determine the minimal number of facets, and estimate the minimal number of vertices, of a convex d-polytope P having no plane shadow boundary with respect to parallel illumination (this property is related to the inclusion [CP] ⊂ int(ΠP)).

Keywords

52A2052B11
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 39 , Issue 4 , 01 December 1996 , pp. 448 - 459
Copyright
Copyright © Canadian Mathematical Society 1996

References

[BF] Bonnesen, T., Fenchel, W., Théorie der konvexen Kôrper, Springer, Berlin 1934; korr. Nachdruck 1974; Chelsea, New York, 1948 (Engl, transi.: Theory of convex bodies, BCS Associates, Moscow, Idaho, 1987).Google Scholar
[Bu] Busemann, H., A theorem on convex bodies of the Brunn-Minkowski type, Proc. Nat. Acad. Sci. U.S.A. 35(1949), 27–31.Google Scholar
[BES] Busemann, H., Ewald, G., Shephard, G. C., Convex bodies and convexity on Grassmann cones I-IV, Math. Ann. 151(1963), 1–41.Google Scholar
[Fa] Falconer, K. J., Applications of a result on spherical integration to the theory of convex sets, Amer. Math. Monthly 90(1983), 690–693.Google Scholar
[Fe] Fédérer, H., Geometric Measure Theory, Grundlehren Math. Wiss. 153 Springer-Verlag, Berlin- Heidelberg-New York, 1969.Google Scholar
[Fu] Funk, P., ÛberFlâchen mit lauter geschlossenen geodâtischen Linien, Math. Ann. 74(1913), 278–300.Google Scholar
[Ga] Gardner, R. J., Geometric Tomography, Cambridge University Press, 1996.Google Scholar
[GW] Goodey, P., Weil, W., Zonoids and generalizations, In: Handbook of Convex Geometry B, (eds. Gruber, P. M. and Wills, J. M.), North-Holland, Amsterdam-London-New York-Tokyo, 1993 1297-1326.Google Scholar
[Gr 77.] Gruber, P. M., Die meisten konvexen Kôrper sind glatt, aber nicht zu glatt, Math. Ann. 229(1977), 259–266.Google Scholar
[Gr 85.] Gruber, P. M., Results of Baire category type in convexity, In: Discrete Geometry and Convexity, (eds. Goodman, J. E., Lutwak, E., Malkevitch, J., Pollack, R.), Annals New York Acad. Sci. 440(1985), 163–169.Google Scholar
[Gr 93.] Gruber, P. M., Baire categories in convexity, In: Handbook of Convex Geometry, (eds. Gruber, P. M. and Wills, J. M.), North-Holland, Amsterdam-London-New York-Tokyo 1993, 1327-1346.Google Scholar
[GH] Gruber, P. M. and Hôbinger, J., Kennzeichnungen von Ellipsoiden mit Anwendungen, In: Jahrbuch Überblicke Math. 1976 Bibliogr. Inst. Mannheim, 1976, 9–29.Google Scholar
[Grù] Gninbaum, B., Convex Poly topes, Interscience, London-New York-Sydney, 1967.Google Scholar
[Ha 51.] Hammer, P. C., Convex bodies associated with a convex body, Proc. Amer. Math. Soc. 2(1951), 781— 793.Google Scholar
[Ha 54.] Hammer, P. C., Diameters of convex bodies, Proc. Amer. Math. Soc. 5(1954), 304—306.Google Scholar
[Ha 63.] Hammer, P. C., Convex curves of constant Minkowski breadth, In: Convexity, (ed. Klee, V. L.), Proc. Sympos. Pure Math. 7, 291-304, Amer. Math. Soc, Providence, R.I., 1963.Google Scholar
[Kl] Klee, V., Some new results on smoothness and rotundity in normed linear spaces, Math. Ann. 139(1959), 51–63.Google Scholar
[LP] Lifshitz, I. M., Pogorelov, A. V., On the determination of Fermi surfaces and electron velocities in metals by the oscillation of magnetic susceptibility (in Russian), Dokl. Akad. Nauk SSSR 96(1954), 1143–1145.Google Scholar
[Lu] Lutwak, E., Intersection bodies and dual mixed volumes, Advances in Math. 71(1988), 232—261.Google Scholar
[MM] Makai, E. Jr., and Martini, H., The cross-section body, plane sections of convex bodies and approximation of convex bodies, I and II, Geom. Dedicata, to appear.Google Scholar
[MMO] Makai, E. Jr., Martini, H., Odor, T., Maximal sections and centrally symmetric bodies, Manuscript, 1994.Google Scholar
[Ma 89.] Martini, H., On inner quermasses of convex bodies, Arch. Math. 52(1989), 402–406.Google Scholar
[Ma 92.] Martini, H., Extremal equalities for cross-sectional measures of convex bodies, Proc. 3rd Geometry Congress, (Thessaloniki 1991), Aristoteles Univ. Press, Thessaloniki, 1992, 285–296.Google Scholar
[Ma 94.] Martini, H., Cross-sectional measures, In: Intuitive Geometry, (eds. Bôrôczky, K. and Fejes Toth, G.), Coll. Math. Soc. J. Bolyai 63, North Holland, Amsterdam-London-New York, 1994, 269–310.Google Scholar
[Pe 52.] Petty, C. M., On Minkowski geometries, Ph. D. dissertation, Univ. South California, Los Angeles, 1952.Google Scholar
[Pe 61.] Petty, C. M., Centroid surfaces, Pacific J. Math. 11(1961), 1535-1547.Google Scholar
[Pe 83.] Petty, C. M., Ellipsoids, In: Convexity and its Applications, (eds. Gruber, P. M. and Wills, J. M.), Birkhàuser, Basel-Boston-Stuttgart 1983, 264-276.Google Scholar
[S W] Schneider, R. and Weil, W., Zonoids and related topics, In: Convexity and its applications, (eds. Gruber, P. M. and Wills, J. M.), Birkhàuser, Basel 1983 296–317.Google Scholar
[PC] Petty, C. M. and Crotty, J. M., Characterizations of spherical neighbourhoods, Canad. J. Math. 22(1970), 431–435.Google Scholar
[Sh] Shephard, G. C., Sections and projections of convex poly topes, Mathematika 19(1972), 144–162.Google Scholar
[Za 91a] Zamfirescu, T., Baire categories in convexity, Atti Sem. Mat. Fis. Univ. Modena 39(1991), 139–164.Google Scholar
[Za 91b] Zamfirescu, T., On two conjectures of Franz Hering about convex surfaces, Discrete Comput. Geom. 6 (1991), 171–180.Google Scholar