Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T07:35:20.396Z Has data issue: false hasContentIssue false
  • English
  • Français

On Basis Constants and Duality in Banach Spaces

Published online by Cambridge University Press:  20 November 2018

Leonard E. Dor
Leonard E. Dor*
Affiliation:
Department of Mathematics, University of Illinois, Urbana, Illinois 61801
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Every Banach space with a non-shrinking (unconditional) basis (Xi) can be renormed so that the biorthogonal sequence has a much smaller (unconditional) basis constant than (xi). On the other hand, if the unconditional constant of 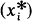is C < 2 then the unconditional constant of (xi) is at most C/(2—C). This estimate is sharp.

Keywords

46B1046B15Non-shrinking basisbiorthogonal functionalsbasis constantunconditional constant
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 22 , Issue 4 , 01 December 1979 , pp. 459 - 465
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Davis, W. J., Dean, D. W., Lin, B-L., Bibasic sequences and norming basic sequences, Transactions AMS 176 (1973), 89-102.Google Scholar
2. Davis, W. J., Johnson, W. B., A renaming of nonreflexive spaces, Proc. AMS 37 (1973), 486-488.Google Scholar
3. Lindenstrauss, J., Tzafriri, L., Classical Banach spaces I, Springer-Verlag, Berlin 1977.Google Scholar
4. Singer, I., On the constants of basic sequences in Banach spaces, Studia Math. 31 (1968), 125-134.Google Scholar
5. Singer, I., Bases in Banach spaces I, Springer-Verlag, Berlin-Heidelberg, New York 1970.Google Scholar