Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-29T02:04:34.890Z Has data issue: false hasContentIssue false
  • English
  • Français

On an Interpolation Theorem of Zygmund and Koizumi

Published online by Cambridge University Press:  20 November 2018

H. P. Heinig
H. P. Heinig*
Affiliation:
McMaster University, Hamilton, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (X, 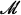, μ) and (Y, 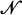, ν) be two σ-finite measure spaces. An operator T, defined by h = Tf, which maps functions on X into functions on Y is called quasilinear if T(f+g) is uniquely defined whenever Tf and Tg are defined, and if

1.1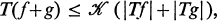

where 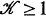is independent of f and g. If 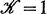the operator T is called sublinear.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 13 , Issue 2 , June 1970 , pp. 221 - 226
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Koizumi, S., On singular integrals I, Proc. Jap. Acad. 34 (1958), 193-198.Google Scholar
2. Koizumi, S., On the Hilbert transform I, J. Fac. Sci. Hokkaido Univ. Ser. I, XIV (1958-59), 153-224.Google Scholar
3. Zygmund, A., Trigonometric series, Cambridge Univ. Press, Vol. I, II, 1959.Google Scholar
4. Zygmund, A., On a theorem of Marcinkiewicz concerning interpolation of operations, J. de Math. 35 (1956), 223-248.Google Scholar