Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-25T16:47:23.617Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Theorem of Rav Concerning Egyptian Fractions

Published online by Cambridge University Press:  20 November 2018

William A. Webb
William A. Webb*
Affiliation:
Washington State University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Problems involving Egyptian fractions (rationals whose numerator is 1 and whose denominator is a positive integer) have been extensively studied. (See [1] for a more complete bibliography). Some of the most interesting questions, many still unsolved, concern the solvability of

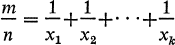
where k is fixed.

In [2] Rav proved necessary and sufficient conditions for the solvabilty of the above equation, as a consequence of some other theorems which are rather complicated in their proofs. In this note we give a short, elementary proof of this theorem, and at the same time generalize it slightly.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 18 , Issue 1 , April 1975 , pp. 155 - 156
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Bleicher, M. N., A new algorithm for the expansion of Egyptian fractions, J. of Number Theory, Vol. 4 (1972), 342-382.Google Scholar
2. Rav, Y., On the representation of a rational number as a sum of a fixed number of unit fractions, J. Reine Angew. Math. 222 (1966), 207-213.Google Scholar
3. Stewart, B. M. and Webb, W. A., Sums of fractions with bounded numerators, Can. J. Math., 18 (1966), 999-1003.Google Scholar