Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T18:18:36.290Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Theorem of Niven

Published online by Cambridge University Press:  20 November 2018

R. Sita Rama Chandra Rao  and
G. Sri Rama Chandra Murty
R. Sita Rama Chandra Rao
Affiliation:
Department of Mathematics, Andhra University, Waltair 530 003, India
G. Sri Rama Chandra Murty
Affiliation:
Department of Mathematics, Andhra University, Waltair 530 003, India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [4], Niven proved that the set A of integers 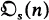for all s ≥ l and all n ≥ 1 has density zero, 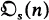being the sum of the sth powers of all positive divisors of n. However his argument contains a mistake (see Remark 1). In this paper we give a proof of Niven's result and establish several related results, one of which generalizes a result of Dressier (See Theorem 3 and Remark 2).

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 22 , Issue 1 , 01 March 1979 , pp. 113 - 115
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Dickson, L. E., History of the Theory of Numbers, Vol. I, Chelsea Publishing Company (reprinted), New York, 1952.Google Scholar
2. Dressier, R. E., On a Theorem of Niven, Canad. Math. Bull., 17 (1), (1974), pp. 109-110.Google Scholar
3. Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers, Oxford University Press, Oxford, Fourth edition (1960).Google Scholar
4. Niven, I., The Asymptotic density of sequences, Bull. A.M.S., 57 (1951), pp. 420-434.Google Scholar
5. Niven, I. and Zuckermann, H. S., An Introduction to the Theory of Numbers, Wiley Eastern Limited, New Delhi-Bangalore, Third edition (1972).Google Scholar