Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T13:42:14.320Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Solution of the Hammerstein Equation with Singular Normal Kernels

Published online by Cambridge University Press:  20 November 2018

Charles G. Costley
Charles G. Costley*
Affiliation:
McGill University, Montreal, Quebec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider here the equation

1

This equation was first studied by Hammerstein [4] under the assumption that the linear operator

2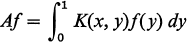

is selfadjoint and completely continuous. V. Nemytsky [5] and M. Golomb [3] dropped the assumption that A be selfadjoint and positive. M. Vainberg [6] considered (among other cases) the case in which A is a bounded operator generated by a Carleman kernel. The kernels considered in this work do not necessarily generate bounded, completely continuous or selfadjoint, operators.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 13 , Issue 4 , December 1970 , pp. 415 - 421
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Carleman, T., Sur les équations intégrales singulières à noyau réel et symmétrique, Uppsala, 1923.Google Scholar
2. Costley, C. G., On singular normal integral equation, Canad. Math. Bull. (2) 13 (1970), 199-203.Google Scholar
3. Golomb, M., Zur Theorie der nicht linear en Integralgleichungen, Integralgleichungs System and allgemeinen Funktional-gleichungen, Math. Z. 39, 1934.Google Scholar
4. Hammerstein, A., Nichtlinear Integralgleichungen nebst Anwendungen, Acta Math. 54 (1930), 117-176.Google Scholar
5. Nemytsky, V., Théorèmes d'existance et d'unicite des solutions de quelques équations intégrales non-linéaires, Mat. Sb. 41, 1934.Google Scholar
6. Vainberg, M. M., Variational methods for the study of non-linear operators, Holden-Day, San Francisco, 1964.Google Scholar
7. Stone, M. H., Linear operators in Hilbert Space, Amer. Math. Soc., Colloq. Publication 1932.Google Scholar