Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Schinzel, A.
1997.
The Mathematics of Paul Erdös I.
Vol. 13,
Issue. ,
p.
151.
Dubickas, A.
1999.
On the order of vanishing at 1 of a polynomial.
Lithuanian Mathematical Journal,
Vol. 39,
Issue. 4,
p.
365.
Cipu, Mihai
2004.
Upper Bounds for Norms of Products of Binomials.
LMS Journal of Computation and Mathematics,
Vol. 7,
Issue. ,
p.
37.
Schinzel, Andrzej
2013.
The Mathematics of Paul Erdős I.
p.
263.
Bourgain, Jean
and
Chang, Mei-Chu
2018.
On a paper of Erdös and Szekeres.
Journal d'Analyse Mathématique,
Vol. 136,
Issue. 1,
p.
253.
Billsborough, C.
Freedman, M.
Hart, S.
Kowalsky, G.
Lubinsky, D.
Pomeranz, A.
and
Sammel, A.
2021.
On lower bounds for Erdős-Szekeres products.
Proceedings of the American Mathematical Society,
Vol. 149,
Issue. 10,
p.
4233.
Hauke, Manuel
2024.
On the asymptotic behaviour of Sudler products for badly approximable numbers.
Journal of Mathematical Analysis and Applications,
Vol. 531,
Issue. 1,
p.
127737.


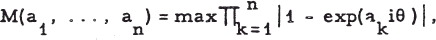
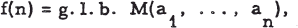
 ,
, 