Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-16T16:10:00.108Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Parametrized Levi Problem Involving One Complex Variable

Published online by Cambridge University Press:  20 November 2018

Bruce Gilligan
Bruce Gilligan*
Affiliation:
Department of Mathematics and Statistics, University of Regina Regina, Saskatchewan Canada S4S 0A2
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The classical Levi problem in several complex variables characterizes domains of holomorphy in terms of a boundary condition called pseudo convexity. The purpose of this note is to give a characterization of those domains D in ℂ×ℝ, where one can always solve the 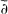-problem with C∞ parameters, in terms of a certain kind of convexity condition on their boundaries.

Keywords

30G30
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 26 , Issue 3 , 01 September 1983 , pp. 324 - 327
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Andreotti, A. and Grauert, H., Théorèmes de finitude pour la cohomologie des espaces complexes, Bull. Soc. Math. France 90 (1962), 193-259.Google Scholar
2. Gunning, R. C. and Rossi, H., Analytic Functions of Several Complex Variables, Prentice- Hall, Englewood Cliffs, NJ, 1965.Google Scholar
3. Hormander, L., On the existence and regularity of solutions of linear pseudo-differential equations, Enseignement Math. 17 (1971), 99-163.Google Scholar
4. Jurchescu, M., Variétés mixtes, (Seminar on Complex Analysis, Bucharest, 1976), LNM 743, Springer-Verlag, New York-Berlin-Heidelberg, 1979, 431-448.Google Scholar
5. Jurchescu, M., mixtes, Espaces, Fifth Romanian-Finnish Seminar on Complex Analysis, Bucharest, 1981.Google Scholar
6. Malgrange, B., Existence et approximation des solutions des équations aux dérivées partielles et des équations de convolution, Ann. Inst. Fourier Grenoble. 6 (1955–56), 271-355.Google Scholar
7. Rea, C., Le problème de Cauchy-Riemann pour les structures mixtes, Ann. Scuola Norm. Sup. Pisa (3) 22 (1968), 695–7_27.Google Scholar
8. Rea, C., Parametrized operator on pseudoconvex sets, Ann. Mat. Pura Appl. (IV) 60 (1976), 161-175.Google Scholar
9. Treves, F., Applications of distributions to PDE theory, Amer. Math. Monthly 77 (1970), 241-248.Google Scholar