Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-22T05:24:55.672Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Paper by M. Iosifescu and S. Marcus

Published online by Cambridge University Press:  20 November 2018

C. J. Neugebauer
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we will construct an example showing that the problem posed in [1] has a negative answer. Two more theorems on the subject treated in [1] will be included.

Let Io = [0, 1], R the reals, and let, for A ⊂ R, Ao be the interior of A. Let {xn} be a sequence in [0, 1> such that 0 = x1 < x2 < … and lim xn = 1. For each n, let In be closed interval having x as its midpoint (except for n = 1 in which case x1 is the left endpoint of I1) such that In ∩ Im= ϕ, and the metric density relative to Io of 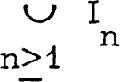at 1 is zero. Let Jn be a closed interval in In concentric with In (except for n = 1, where J1 has x1 as its left endpoint) whose length is half that of In

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 6 , Issue 3 , 01 September 1963 , pp. 367 - 371
Copyright
Copyright © Canadian Mathematical Society 1963

References

1. Iosifescu, M. and Marcus, S., Sur un problème de P. Scherk concernant la somme de carrés de deux dériées, Canad. Math. Bull. vol. 5, no. 2 (1962), pp. 129-132.Google Scholar
2. Saks, S., Theory of the Integral, Warszawa-Lwow, 1937.Google Scholar