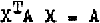Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Marcus, Marvin
and
Khan, Nisar A.
1960.
A Note an a Group Defined by a Quadratic Form.
Canadian Mathematical Bulletin,
Vol. 3,
Issue. 2,
p.
143.
PHILIPS, T.O.
and
WIGNER, E.P.
1968.
Group Theory and its Applications.
p.
631.
Belinfante, J. G. F.
and
Winternitz, P.
1971.
One-Parameter Subgroups of Unitary Groups with Indefinite Metric and in Particular of the Conformal Group.
Journal of Mathematical Physics,
Vol. 12,
Issue. 6,
p.
1041.
Riehm, Carl
1974.
The equivalence of bilinear forms.
Journal of Algebra,
Vol. 31,
Issue. 1,
p.
45.
Kalnins, E. G.
and
Miller, Willard
1975.
Lie theory and separation of variables. 8. Semisubgroup coordinates for Ψt
t − Δ2Ψ = 0.
Journal of Mathematical Physics,
Vol. 16,
Issue. 12,
p.
2507.
Kalnins, E. G.
and
Miller, W.
1977.
Lie theory and the wave equation in space–time. 3. Semisubgroup coordinates.
Journal of Mathematical Physics,
Vol. 18,
Issue. 2,
p.
271.
Burgoyne, N
and
Cushman, R
1977.
Conjugacy classes in linear groups.
Journal of Algebra,
Vol. 44,
Issue. 2,
p.
339.
Boyer, C. P.
and
Kalnins, E. G.
1977.
Symmetries of the Hamilton–Jacobi equation.
Journal of Mathematical Physics,
Vol. 18,
Issue. 5,
p.
1032.
Moshinsky, M.
and
Winternitz, P.
1980.
Quadratic Hamiltonians in phase space and their eigenstates.
Journal of Mathematical Physics,
Vol. 21,
Issue. 7,
p.
1667.
Patera, J.
and
Rousseau, C.
1982.
Complex orthogonal and symplectic matrices depending on parameters.
Journal of Mathematical Physics,
Vol. 23,
Issue. 5,
p.
705.
Djoković, D. Ž.
Patera, J.
Winternitz, P.
and
Zassenhaus, H.
1983.
Normal forms of elements of classical real and complex Lie and Jordan algebras.
Journal of Mathematical Physics,
Vol. 24,
Issue. 6,
p.
1363.
Patera, J.
Winternitz, P.
and
Zassenhaus, H.
1983.
Maximal abelian subalgebras of real and complex symplectic Lie algebras.
Journal of Mathematical Physics,
Vol. 24,
Issue. 8,
p.
1973.
Friedlein, Heinz-Reiner
1984.
Normalformen f�r Bewegungen in hyperbolischen R�umen.
Journal of Geometry,
Vol. 23,
Issue. 1,
p.
61.
Iosifescu, Mircea
and
Scutaru, Horia
1986.
Conformal Groups and Related Symmetries Physical Results and Mathematical Background.
Vol. 261,
Issue. ,
p.
48.
Knüppel, Frieder
and
Nielsen, Klaus
1987.
On products of two involutions in the orthogonal group of a vector space.
Linear Algebra and its Applications,
Vol. 94,
Issue. ,
p.
209.
Pierce, Stephen
1992.
Chapter 4:algebraic sets, polynomials, and other functions.
Linear and Multilinear Algebra,
Vol. 33,
Issue. 1-2,
p.
31.
Alali, M. I.
Hering, C. H.
and
Schäeffer, J.
2001.
On the Characters of the Maximal Subgroup <f 1> Sp 4 ( q ) of the Symplectic Group Sp 4(q), q-Even.
Acta Mathematica Sinica, English Series,
Vol. 17,
Issue. 4,
p.
621.
Grudzinski, Olaf v.
Knüppel, Frieder
and
Nielsen, Klaus
2009.
Supernormal mappings: Part 1. Orthogonally indecomposable modules and applications.
Linear Algebra and its Applications,
Vol. 431,
Issue. 1-2,
p.
39.