Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-09T08:52:05.041Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Few Diophantine Equations Related to Fermat’s Last Theorem

Published online by Cambridge University Press:  20 November 2018

O. Kihel  and
C. Levesque
O. Kihel
Affiliation:
Dept. of Math. and Comp. Sc., University of Lethbridge, Lethbridge, Alberta, T1K 3M4
C. Levesque
Affiliation:
Dép. Mathématiques et CICMA, Université Laval, Québec, G1K 7P4
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We combine the deep methods of Frey, Ribet, Serre and Wiles with some results of Darmon, Merel and Poonen to solve certain explicit diophantine equations. In particular, we prove that the area of a primitive Pythagorean triangle is never a perfect power, and that each of the equations 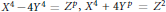${{X}^{4}}\,-\,4{{Y}^{4}}\,=\,{{Z}^{p}},\,{{X}^{4}}\,+\,4{{Y}^{p}}\,=\,{{Z}^{2}}$ has no non-trivial solution. Proofs are short and rest heavily on results whose proofs required Wiles’ deep machinery.

Keywords

11D41Diophantine equations
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 2 , 01 June 2002 , pp. 247 - 256
Copyright
Copyright © Canadian Mathematical Society 2002

References

[B-C-D-T] Breuil, C., Conrad, B., Diamond, P. and Taylor, R., Result announcement. Notices Amer. Math. Soc. (9) 46(1999), 863.Google Scholar
[C1] Cao, Z., The Diophantine equation x4 − Dy2 = 1. (Chinese) J. Harbin Inst. Tech. (4) 13 (1981), 13–1981; II. J. Harbin Inst. Tech. (3) 15 (1983), 15–1983.Google Scholar
[C2] Cao, Z., The Diophantine equations x4 − y4 = zp and x4 + 1 = dyq. C. R. Math. Rep. Acad. Sci. Canada (1) 21 (1999), 21–1999.Google Scholar
[C-P] Cao, Z. and Pan, J., The Diophantine equation x2p − Dy2 = 1 and the Fermat quotient Qp(m). J. Harbin Inst. Tech. 25 (1993), 25–1993.Google Scholar
[D1] Darmon, H., The equations xn + yn = z2 and xn + yn = z3 . Intern. Math. Res. Notices (10) 1993, 263–274.Google Scholar
[D2] Darmon, H., The equation x4 − y4 = zp . C. R. Math. Rep. Acad. Sci. Canada 15 (1993), 15–1993.Google Scholar
[D-M] Darmon, H. and Merel, L., Winding quotients and some variants of Fermat's Last Theorem. J. Reine Angew. Math. 490 (1997), 490–1997.Google Scholar
[De] Dénes, P., Uber die Diophantische Gleichung xl + yl = czl . Acta Math. 88 (1952), 88–1952.Google Scholar
[E-M] Esmonde, J. and Murty, R., Problems in Algebraic Number Theory. Graduate Texts in Math. 190, Springer-Verlag, 1999.Google Scholar
[L] Le, M., A note on the Diophantine equation xp−1 − 1 = pyq . C. R. Math. Rep. Acad. Sci. Canada. 15 (1993), 15–1993.Google Scholar
[O-T] Osada, H. and Terai, N., Generalization of Lucas’ theorem for Fermat quotient. C. R. Math. Rep. Acad. Sci. Canada 11 (1989), 11–1989.Google Scholar
[P] Powell, B., Sur l’équation diophantienne x4 ± y4 = zp . Bull. Sci.Math. 107 (1983), 107–1983.Google Scholar
[Riben] Ribenboim, P., Catalan's Conjecture. Academic Press, 1994.Google Scholar
[Ribet] Ribet, K. A., On the equation ap + 2αbp + cp = 0. Acta Arith. 79 (1997), 79–1997.Google Scholar
[S] Serre, J.-P., Sur les représentations modulaires de degré 2 de Gal(). Duke Math. J. 54 (1987), 54–1987.Google Scholar
[T] Taylor, R. L. and Wiles, A., Ring theoretic properties of certain Hecke algebras. Ann. of Math. 141 (1995), 141–1995.Google Scholar
[W] Wiles, A., Modular elliptic curves and Fermat's Last Theorem. Ann. of Math. 141 (1995), 141–1995.Google Scholar