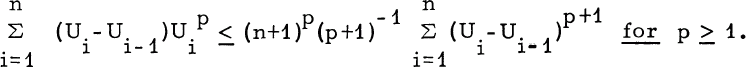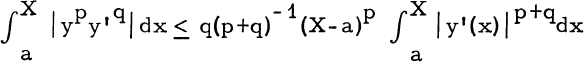Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mitrinović, Dragoslav S.
1970.
Analytic Inequalities.
p.
27.
Beesack, P. R.
1971.
Integral Inequalities Involving a Function and its Derivative.
The American Mathematical Monthly,
Vol. 78,
Issue. 7,
p.
705.
Shum, Daniel T.
1975.
On a class of new inequalities.
Transactions of the American Mathematical Society,
Vol. 204,
Issue. 0,
p.
299.
Lee, Cheng-Shyong
1980.
On Some Generalization of Inequalities of Opial, Yang and Shum.
Canadian Mathematical Bulletin,
Vol. 23,
Issue. 1,
p.
71.
Pachpatte, B.G
1987.
A note on Opial and Wirtinger type discrete inequalities.
Journal of Mathematical Analysis and Applications,
Vol. 127,
Issue. 2,
p.
470.
Mitrinović, D. S.
Pečarić, J. E.
and
Fink, A. M.
1991.
Inequalities Involving Functions and Their Integrals and Derivatives.
p.
114.
Ju-Da, Li
1992.
Opial-type integral inequalities involving several higher order derivatives.
Journal of Mathematical Analysis and Applications,
Vol. 167,
Issue. 1,
p.
98.
Agarwal, Ravi P.
1992.
Opial's and wirtinger's type discrete inequalities in two independent variables.
Applicable Analysis,
Vol. 43,
Issue. 1-2,
p.
47.
Agarwal, R.P.
and
Pang, P.Y.H.
1995.
Opial-type inequalities involving higher order differences.
Mathematical and Computer Modelling,
Vol. 21,
Issue. 5,
p.
49.
Agarwal, Ravi P.
and
Pang, Peter Y. H.
1995.
Opial Inequalities with Applications in Differential and Difference Equations.
p.
283.
Alzer, Horst
1995.
Note on a discrete Opial-type inequality.
Archiv der Mathematik,
Vol. 65,
Issue. 3,
p.
267.
Agarwal, Ravi P.
and
Pang, Peter Y.H.
1995.
Sharp discrete inequalities inn independent variables.
Applied Mathematics and Computation,
Vol. 72,
Issue. 2-3,
p.
97.
Agarwal, Ravi P.
and
Pang, Peter Y.H.
1996.
Discrete opial-type inequalities involving higher order partial differences.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 27,
Issue. 4,
p.
429.
Milovanović, Gradimir V.
and
Milovanović, Igor Ž.
1998.
Recent Progress in Inequalities.
p.
289.
2005.
Mathematical Inequalities.
Vol. 67,
Issue. ,
p.
485.
2005.
Mathematical Inequalities.
Vol. 67,
Issue. ,
p.
565.
Gao, Peng
2010.
On l p norms of weighted mean matrices.
Mathematische Zeitschrift,
Vol. 264,
Issue. 4,
p.
829.
Vi Nhan, Nguyen Du
Duc, Dinh Thanh
Tuan, Vu Kim
and
Huy Vu, Nguyen Du
2014.
Inequalities for differences and their applications.
Journal of Difference Equations and Applications,
Vol. 20,
Issue. 9,
p.
1319.


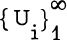 be a non-decreasing sequence of non-negative numbers, and let U
be a non-decreasing sequence of non-negative numbers, and let U