Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T06:56:17.644Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Class of Singular Integral Operators With Rough Kernels

Published online by Cambridge University Press:  20 November 2018

Ahmad Al-Salman
Ahmad Al-Salman*
Affiliation:
Department of Mathematics, Yarmouk University, Irbid, Jordan email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

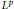In this paper, we study the ${{L}^{p}}$ mapping properties of a class of singular integral operators with rough kernels belonging to certain block spaces. We prove that our operators are bounded on 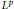${{L}^{p}}$ provided that their kernels satisfy a size condition much weaker than that for the classical Calderón–Zygmund singular integral operators. Moreover, we present an example showing that our size condition is optimal. As a consequence of our results, we substantially improve a previously known result on certain maximal functions.

Keywords

42B2042B1542B25Singular integralsRough kernelsSquare functionsMaximal functionsBlock spaces
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 1 , 01 March 2006 , pp. 3 - 10
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Al-Hasan, A. and Fan, D., A singular integral operator related to block spaces. Hokkaido Math. J. 28(1999), 285–299.Google Scholar
[2] Al-Qassem, H. and Pan, Y., Lp estimates for singular integrals with kernels belonging to certain block spaces. Rev. Mat. Iberoamericana (18) 3(2002) 701–730.Google Scholar
[3] Al-Qassem, H., Al-Salman, A. and Pan, Y., Singular integrals associated to homogeneous mappings with rough kernels. Hokkaido Math. J. 33(2004), 551–569.Google Scholar
[4] Al-Qassem, H. and Al-Salman, A., A note on Marcinkiewicz integral operators. J. Math. Anal. Appl. 282(2003) 698–710.Google Scholar
[5] Al-Salman, A. and Pan, Y., Singular integrals with rough kernels in L log+ L(S n–1). J. London. Math. Soc. (2) 66(2002), 153–174.Google Scholar
[6] Al-Salman, A. and Al-Qassem, H., Integral operators of Marcinkiewicz type. J. Integral Equations Appl. (4) 14(2002).Google Scholar
[7] Calderón, A. and Zygmund, A., On existence of certain singular integrals. Acta. Math. 88(1952), 85–129.Google Scholar
[8] Chen, L. and Lin, H., A maximal operator related to a class of singular integrals. Illinois J. Math. (1) 34(1990), 120–126.Google Scholar
[9] Connett, W. C., Singular integrals near L 1 . In: Harmonic analysis in Euclidean spaces. Proc. Sympos. Pure Math. 35, Amer.Math. Soc., Providence, RI, 1979, pp. 163–165.Google Scholar
[10] Duoandikoetxea, J. and Rubio de Francia, J. L. , Maximal and singular integral operators via Fourier transform estimates. Invent. Math. 84(1986), 541–561.Google Scholar
[11] Fan, D. and Pan, Y., Singular integrals with rough kernels supported by subvarieties. Amer. J. Math. 119(1997), 799–839.Google Scholar
[12] Keitoku, M. and Sato, E., Block spaces on the unit sphere in R n . Proc. Amer. Math. Soc. 119(1993), 453–455.Google Scholar
[13] Lu, S., Taibleson, M. and Weiss, G., Spaces Generated by Blocks. Beijing Normal University Press, 1989, Beijing.Google Scholar
[14] Ricci, F. and Weiss, G., A characterization of H 1(S n–1 ). In: Harmonic analysis in Euclidean spaces. Proc. Sympos. Pure Math. 35, Amer.Math. Soc., Providence, RI, 1979, pp. 289–294.Google Scholar
[15] Stein, E. M., Singular integrals and differentiability properties of functions. Princeton University Press, Princeton New Jersey, 1970.Google Scholar
[16] Stein, E. M., Harmonic Analysis: Real-Variable Methods, Orthogonality and Oscillatory Integrals. Princeton University Press, Princeton, New Jersey, 1993.Google Scholar