Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T18:44:01.621Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Class of Nonparametric Tests for Independence—Bivariate Case(1)

Published online by Cambridge University Press:  20 November 2018

M. S. Srivastava
M. S. Srivastava*
Affiliation:
University of Toronto, Toronto, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let(X1, Y1), (X2, Y2),…, (Xn, Yn) be n mutually independent pairs of random variables with absolutely continuous (hereafter, a.c.) pdf given by

(1)

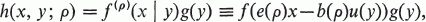
where f(ρ) denotes the conditional pdf of X given Y, g(y) the marginal pdf of Y, e(ρ)→ 1 and b(ρ)→0 as ρ→0 and,

(2)

We wish to test the hypothesis

(3)

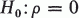
against the alternative

(4)

For the two-sided alternative we take — ∞< b < ∞. A feature of the model (1) is that it covers both-sided alternatives which have not been considered in the literature so far.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 16 , Issue 3 , September 1973 , pp. 337 - 342
Copyright
Copyright © Canadian Mathematical Society 1973

Footnotes

(1)

Research supported partially by Canada Council and National Research Council of Canada.

References

1. Bhuchongkul, S., A class of non-parametric tests for independence in Bivariate populations, Ann. Math. Statist. 35 (1964) 138–149.Google Scholar
2. Chernoff, H., Gastwirth, J. L., and Johns, M. V., Asymptotic distribution of linear combinations of functions of order statistics with applications to estimation, Ann. Math. Statist. 38 (1967), 52–72.Google Scholar
3. Cramer, H., Mathematical methods of statistics, Princeton Univ. Press, Princeton, N.J., 1946.Google Scholar
4. Farlie, D. J. G., The asymptotic efficiency of Daniel’s generalized correlation coefficients, J. Roy. Statist. Soc. Ser. B. 23 (1961) 128–142.Google Scholar
5. Hájek, J. and Šidák, Z., Theory of rank tests, Academic Press, New York, 1967.Google Scholar
6. Konijn, H. S., On the power of certain tests for independence in bivariate populations, Ann. Math. Statist. 27 (1956), 300–323. Correction 27 (1958), p. 935.Google Scholar
7. Moore, D. S., An elementary proof of asymptotic normality of linear functions of order statistics, Ann. Math. Statist. 39 (1968), 263–265.Google Scholar