Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-05T01:02:49.637Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical Semigroups That Are Not Intersections of d-Squashed Semigroups

Published online by Cambridge University Press:  20 November 2018

M. A. Moreno ,
J. Nicola ,
E. Pardo  and
H. Thomas
M. A. Moreno
Affiliation:
Departamento de Matemáticas, Facultad de Ciencias, Universidad de Cádiz, Campus de Puerto Real, 11510 Puerto Real (Cádiz), Spain e-mail: [email protected]@uca.es
J. Nicola
Affiliation:
Département de Mathématiques, Université de Genève, Switzerland e-mail: [email protected]
E. Pardo
Affiliation:
Departamento de Matemáticas, Facultad de Ciencias, Universidad de Cádiz, Campus de Puerto Real, 11510 Puerto Real (Cádiz), Spain e-mail: [email protected]@uca.es
H. Thomas
Affiliation:
Department of Mathematics and Statistics, University of New Brunswick, Fredericton, NB, E3B 5A3 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We say that a numerical semigroup is $d$-squashed if it can be written in the form

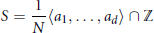$$S\,=\,\frac{1}{N}\langle {{a}_{1}},\,.\,.\,.\,,\,{{a}_{d}}\rangle \,\cap \,\mathbb{Z}$$

for 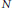$N$, 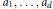${{a}_{1}}\,,\,.\,.\,.\,,\,{{a}_{d}}$ positive integers with 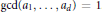$\gcd \left( {{a}_{1}},\,.\,.\,.\,,{{a}_{d}} \right)\,=\,1$. Rosales and Urbano have shown that a numerical semigroup is 2-squashed if and only if it is proportionally modular.

Recent works by Rosales et al. give a concrete example of a numerical semigroup that cannot be written as an intersection of 2-squashed semigroups. We will show the existence of infinitely many numerical semigroups that cannot be written as an intersection of 2-squashed semigroups. We also will prove the same result for 3-squashed semigroups. We conjecture that there are numerical semigroups that cannot be written as the intersection of $d$-squashed semigroups for any fixed $d$, and we prove some partial results towards this conjecture.

Keywords

20M1406F0546L80numerical semigroupsquashed semigroupproportionally modular semigroup
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 4 , 01 December 2009 , pp. 598 - 612
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Elliott, G. and Villadsen, J., Perforated ordered K 0 -groups. Canad. J. Math. 52(2000), no. 6, 1164–1191.Google Scholar
[2] Matoušek, J., Lectures on Discrete Geometry. Graduate Texts in Mathematics 121. Springer-Verlag, New York, 2002.Google Scholar
[3] Rørdam, M. and Villadsen, J., On the ordered K 0 -group of universal free product C*-algebras . K-Theory 15(1998), no. 4, 307–322.Google Scholar
[4] Rosales, J. C. and Branco, M. B., Decomposition of a numerical semigroup as an intersection of irreducible numerical semigroups. Bull. Belg. Math. Soc. Simon Stevin 9(2002), no. 3, 373–381.Google Scholar
[5] Rosales, J. C. and Branco, M. B., Irreducible numerical semigroups. Pacific J. Math. 209(2003), no. 1, 131–143.Google Scholar
[6] Rosales, J. C. and Garcia-Sanchez, P. A., Finitely Generated CommutativeMonoids. Nova Science Publishers, Commack, NY, 1999.Google Scholar
[7] Rosales, J. C., Garcia-Sanchez, P. A., Garcia-Garcia, J. I., and Urbano-Blanco, J. M., Proportionally modular Diophantine inequalities. J. Number Theory 103(2003), no. 2, 281–294.Google Scholar
[8] Rosales, J. C. and Urbano-Blanco, J. M., Proportionally modular diophantine inequalities and full semigroups. Semigroup Forum 72(2006), no. 3, 362–374.Google Scholar
[9] Toms, A., On Strongly Perforated K 0 -Groups of Simple C*-Algebras. Ph.D. Thesis, University of Toronto, 2001.Google Scholar
[10] Toms, A., Strongly perforated K 0 -groups of simple C*-algebras. Canad. Math. Bull. 46(2003), no. 3, 457–472.Google Scholar
[11] Villadsen, J., Simple C*-algebras with perforation. J. Funct. Anal. 154(1998), no. 1, 110–116.Google Scholar