Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cryer, C. W.
1968.
Pivot size in gaussian elimination.
Numerische Mathematik,
Vol. 12,
Issue. 4,
p.
335.
Golub, Gene H.
1969.
Statistical Computation.
p.
365.
Gentleman, W. Morven
1969.
Off-the-Shelf Black Boxes for Programming.
IEEE Transactions on Education,
Vol. 12,
Issue. 1,
p.
43.
Brayton, Robert K.
Gustavson, Fred G.
and
Willoughby, Ralph A.
1970.
Some results on sparse matrices.
Mathematics of Computation,
Vol. 24,
Issue. 112,
p.
937.
Businger, P. A.
1971.
Monitoring the numerical stability of Gaussian elimination.
Numerische Mathematik,
Vol. 16,
Issue. 4,
p.
360.
Wilkinson, J. H.
1971.
Modern Error Analysis.
SIAM Review,
Vol. 13,
Issue. 4,
p.
548.
Bunch, J. R.
1971.
Analysis of the Diagonal Pivoting Method.
SIAM Journal on Numerical Analysis,
Vol. 8,
Issue. 4,
p.
656.
Kincaid, David R.
1974.
On Complex Second-Degree Iterative Methods.
SIAM Journal on Numerical Analysis,
Vol. 11,
Issue. 2,
p.
211.
Nashed, M.Z.
and
Rall, L.B.
1976.
Generalized Inverses and Applications.
p.
771.
Cannarozzi, Agostino A.
and
Laudiero, Ferdinando
1976.
On plastic dynamics of discrete structural models.
Meccanica,
Vol. 11,
Issue. 1,
p.
23.
1977.
Numerical Algebra.
p.
212.
Skeel, Robert D.
1979.
Scaling for Numerical Stability in Gaussian Elimination.
Journal of the ACM,
Vol. 26,
Issue. 3,
p.
494.
Laub, Alan J.
1980.
Information Linkage Between Applied Mathematics and Industry.
p.
57.
Klema, V.
and
Laub, A.
1980.
The singular value decomposition: Its computation and some applications.
IEEE Transactions on Automatic Control,
Vol. 25,
Issue. 2,
p.
164.
Faddeev, D. K.
and
Faddeeva, V. N.
1981.
Computational methods of linear algebra.
Journal of Soviet Mathematics,
Vol. 15,
Issue. 5,
p.
531.
Fairweather, Graeme
1984.
A note on the condition of a matrix.
International Communications in Heat and Mass Transfer,
Vol. 11,
Issue. 2,
p.
191.
Demko, Stephen
1986.
Condition numbers of rectangular systems and bounds for generalized inverses.
Linear Algebra and its Applications,
Vol. 78,
Issue. ,
p.
199.
MARTIN, J. M.
and
HEWER, G. A.
1987.
Smallest destabilizing perturbations for linear systems.
International Journal of Control,
Vol. 45,
Issue. 5,
p.
1495.
Martin, J.
1987.
State-space measures for stability robustness.
IEEE Transactions on Automatic Control,
Vol. 32,
Issue. 6,
p.
509.
Higham, Nicholas J.
1987.
A Survey of Condition Number Estimation for Triangular Matrices.
SIAM Review,
Vol. 29,
Issue. 4,
p.
575.


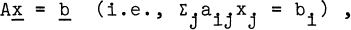
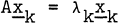
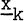 of a given matrix A.
of a given matrix A.