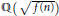Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Poonen, Bjorn
2003.
Squarefree values of multivariable polynomials.
Duke Mathematical Journal,
Vol. 118,
Issue. 2,
Luca, Florian
and
Shparlinski, Igor E.
2007.
Discriminants of Complex Multiplication Fields of Elliptic Curves over Finite Fields.
Canadian Mathematical Bulletin,
Vol. 50,
Issue. 3,
p.
409.
Lee, Jung-Jo
and
Murty, M. Ram
2007.
Dirichlet series and hyperelliptic curves.
Forum Mathematicum,
Vol. 19,
Issue. 4,
Balasuriya, Sanka
Luca, Florian
and
Shparlinski, Igor E.
2007.
Prime Divisors Of Some Recurrence Sequence.
Periodica Mathematica Hungarica,
Vol. 54,
Issue. 2,
p.
215.
Granville, A.
2010.
Rational and Integral Points on Quadratic Twists of a Given Hyperelliptic Curve.
International Mathematics Research Notices,
Cilleruelo, Javier
Luca, Florian
Quirós, Adolfo
and
Shparlinski, Igor E.
2010.
On squares in polynomial products.
Monatshefte für Mathematik,
Vol. 159,
Issue. 3,
p.
215.
Shparlinski, Igor E.
2013.
Advances in Applied Mathematics, Modeling, and Computational Science.
Vol. 66,
Issue. ,
p.
65.
Banks, William D.
and
Shparlinski, Igor E.
2016.
On Coincidences Among Quadratic Fields Generated by the Shanks Sequence.
The Quarterly Journal of Mathematics,
Shparlinski, Igor E.
and
Zhao, Liangyi
2018.
Elliptic curves in isogeny classes.
Journal of Number Theory,
Vol. 191,
Issue. ,
p.
194.
Hasson, Hilaf
and
Obus, Andrew
2018.
THE abc CONJECTURE IMPLIES THE WEAK DIVERSITY CONJECTURE.
Albanian Journal of Mathematics,
Vol. 12,
Issue. 1,
SHPARLINSKI, IGOR E.
2024.
ON QUADRATIC FIELDS GENERATED BY POLYNOMIALS.
Bulletin of the Australian Mathematical Society,
Vol. 109,
Issue. 3,
p.
476.