Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T02:17:17.528Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Upper Bounds for the Eigenvalues of y″ + λpy=0

Published online by Cambridge University Press:  20 November 2018

Rodney D. Gentry
Rodney D. Gentry*
Affiliation:
Department of Mathematics and Statistics, University of Guelph
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The natural modes of a small planar transversal vibration of a fixed string of unit length and tension are determined by the eigenvalues and associated eigenfunctions of the differential equation

(1)

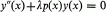
subject to the boundary condition

(2)

where the non-negative function p describes the mass distribution of the string. That the distribution of mass on the string influences the modes of vibration, may be reflected by observing that the eigenvalues determined by the system (1–2) may be considered functions of the density p, λn(p), where λ1(p)<λ2(p)<….

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 18 , Issue 3 , August 1975 , pp. 347 - 351
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Banks, D. O., Bounds for the eigenvalues of some vibrating systems\ Pacific J. Math. 10 (1960), 439-474.Google Scholar
2. Banks, D. O. Upper bounds for the eigenvalues of some vibrating systems, Pacific J. Math. 11 (1961), 1183-1203.Google Scholar
3. Banks, D. O. Bounds for eigenvalues and generalized convexity, Pacific J. Math. 12 (1963), 1031-1052.Google Scholar
4. Banks, D. O. Lower bounds for the eigenvalues of a vibrating string whose density satisfies a Lipschitz condition, Pacific J. Math. 20 (1967), 393-410.Google Scholar
5. Barnes, D., Some isoperimetric inequalities for the eigenvalues of vibrating strings, Pacific J. Math. 29 (1969), 43-61.Google Scholar
6. Beesack, Paul R., A note on an integral inequality, Proc, Amer. Math. Soc. 8 (1957), 875- 879.Google Scholar
7. Beesack, P. R. and Schwarz, B., On zeros of solutions of second order linear differential equations, Canadian J. Math. 8 (1956), 504-515.Google Scholar
8. Courant, R. and Hilbert, D., Methods of Mathematical Physics, Vol. 1, Intersciences Publishers Inc., N.Y. (1966).Google Scholar
9. Gentry, R. and Banks, D. O., Bounds for functions of eigenvalues for vibrating systems, To appear in J. of Mathematical Analysis and Applications.Google Scholar
10. Hardy, G. H., Littlewood, J. E., and Polya, G.., Inequalities, Cambridge University Press (1964).Google Scholar
11. Krein, M. G., On certain problems on the maximum and minimum of characteristic values and on the Lyapunov zones of stability, Amer. Math. Soc. Translation, Ser. 2, Vol. 1 (1955), 163- 187.Google Scholar
12. Schwarz, Binjamin, On the Extrema of the Frequencies of Non-homogeneous Strings with Equimeasurable Density, J. Math, and Mech. V. 10, (1961), 401-422.Google Scholar
13. Tricomi, F. G., Integral Equations, Interscience Publishers, Inc., N.Y., (1967).Google Scholar