Hostname: page-component-f554764f5-rvxtl Total loading time: 0 Render date: 2025-04-18T16:49:20.020Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the X-torsion order of a knot

Published online by Cambridge University Press:  18 March 2025

Dirk Schütz Open the ORCID record for Dirk Schütz [Opens in a new window]
Dirk Schütz*
Affiliation:
Department of Mathematical Sciences, Durham University, Durham, DH1 3LE, United Kingdom
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the X-torsion order of a knot, which is defined in terms of a generalized Lee complex, can be calculated using the reduced Bar-Natan–Lee–Turner spectral sequence. We use this for extensive calculations, including an example of X-torsion order 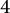$4$.

Keywords

Khovanov homologyX-torsion orderBar-Natan–Lee–Turner spectral sequence
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 6
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alishahi, A. and Dowlin, N., The Lee spectral sequence, unknotting number, and the knight move conjecture . Topol. Appl. 254(2019), 29–38. MR 3894208Google Scholar
Alishahi, A., Unknotting number and Khovanov homology . Pac. J. Math. 301(2019), no. 1, 15–29. MR 4007369Google Scholar
Bar-Natan, D., Fast Khovanov homology computations . J. Knot Theory Ramif. 16(2007), no. 3, 243–255. MR 2320156Google Scholar
Caprau, C., González, N., Lee, C. R. S., Lowrance, A. M., Sazdanović, R., and Zhang, M., On Khovanov homology and related invariants . In: B. Acu, C. Cannizzo, D. McDuff, Z. Myer, Y. Pan and L. Traynor, (eds.), Research directions in symplectic and contact geometry and topology, Association for Women in Mathematics Series, 27, Springer, Cham, 2021, ©2021, pp. 273–292. MR 4417719Google Scholar
Gujral, O. S., Ribbon distance bounds from bar-natan homology and $\alpha$ -homology. Preprint, 2020. arXiv:2011.01190.Google Scholar
Iltgen, D., Lewark, L., and Marino, L., Khovanov homology and rational unknotting. Preprint, 2021. arXiv:2110.15107.Google Scholar
Khovanov, M., Link homology and Frobenius extensions . Fund. Math. 190(2006), 179–190. MR 2232858Google Scholar
Lee, E. S., An endomorphism of the Khovanov invariant . Adv. Math. 197(2005), no. 2, 554–586. MR 2173845Google Scholar
Lewark, L., Marino, L., and Zibrowius, C., Khovanov homology and refined bounds for gordian distances. Preprint, 2024. arXiv:2409.05743 Google Scholar
Lipshitz, R. and Sarkar, S., A mixed invariant of nonorientable surfaces in equivariant Khovanov homology . Trans. Amer. Math. Soc. 375(2022), no. 12, 8807–8849. MR 4504654Google Scholar
Manolescu, C. and Marengon, M., The knight move conjecture is false . Proc. Amer. Math. Soc. 148(2020), no. 1, 435–439. MR 4042864Google Scholar
Sarkar, S., Ribbon distance and Khovanov homology . Algebr Geom. Topol. 20(2020), no. 2, 1041–1058. MR 4092319Google Scholar
Turner, P., Khovanov homology and diagonalizable Frobenius algebras . J. Knot Theory Ramif. 29(2020), no. 1, 1950095, 10. MR 4079621Google Scholar
Zhuang, Z., Knot cobordism and Lee’s perturbation of Khovanov homology . J. Knot Theory Ramif. 31(2022), no. 2, Paper No. 2250012, 6. MR 4420588Google Scholar