Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T23:29:59.907Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on the Vanishing Viscosity Limit in the Yudovich Class

Part of: Incompressible viscous fluids Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  24 April 2020

Christian Seis
Christian Seis*
Affiliation:
Institut für Analysis und Numerik, Westfälische Wilhelms-Universität Münster, Orléans-Ring 10, 48149Münster, Germany
*
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the inviscid limit for the two-dimensional Navier–Stokes equations in the class of integrable and bounded vorticity fields. It is expected that the difference between the Navier–Stokes and Euler velocity fields vanishes in 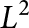$L^2$ with an order proportional to the square root of the viscosity constant 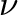$\nu $. Here, we provide an order 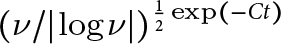$ (\nu /|\log \nu | )^{\frac 12\exp (-Ct)}$ bound, which slightly improves upon earlier results by Chemin.

Keywords

Vanishing viscosityYudovichEulerNavier-StokesstabilityWasserstein

MSC classification

Primary: 35Q30: Navier-Stokes equations
Secondary: 76D09: Viscous-inviscid interaction
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 1 , March 2021 , pp. 112 - 122
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Canadian Mathematical Society 2020

Footnotes

This work is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy EXC 2044–390685587, Mathematics Münster: Dynamics–Geometry–Structure.

References

Abidi, H. and Danchin, R., Optimal bounds for the inviscid limit of Navier-Stokes equations. Asymptot. Anal. 38(2004), 35–46.Google Scholar
Ben-Artzi, M., Global solutions of two-dimensional Navier-Stokes and Euler equations. Arch. Rational Mech. Anal. 128(1994), 329–358. https://doi.org/10.1007/BF00387712CrossRefGoogle Scholar
Chemin, J.-Y., A remark on the inviscid limit for two-dimensional incompressible fluids. Comm. Partial Differential Equations 21(1996), 1771–1779. https://doi.org/10.1080/03605309608821245Google Scholar
Constantin, P., Drivas, T. D., and Elgindi, T. M., Inviscid limit of vorticity distributions in yudovich class. Preprint, 2019. arXiv:1909.04651Google Scholar
Constantin, P. and Wu, J., Inviscid limit for vortex patches. Nonlinearity 8(1995), 735–742.CrossRefGoogle Scholar
Constantin, P. and Wu, J., The inviscid limit for non-smooth vorticity. Indiana Univ. Math. J. 45(1996), 67–81. https://doi.org/10.1512/iumj.1996.45.1960CrossRefGoogle Scholar
Cozzi, E., Vanishing viscosity in the plane for nondecaying velocity and vorticity. SIAM J. Math. Anal. 41(2009), 495–510. https://doi.org/10.1137/080717572CrossRefGoogle Scholar
Cozzi, E., Vanishing viscosity in the plane for nondecaying velocity and vorticity. II. Pacific J. Math. 270(2014), 335–350. https://doi.org/10.2140/pjm.2014.270.335Google Scholar
DiPerna, R. J. and Lions, P. L., Ordinary differential equations, transport theory and Sobolev spaces. Invent. Math. 98(1989), 511–547. https://doi.org/10.1007/BF01393835CrossRefGoogle Scholar
Fournier, N. and Perthame, B., Monge-Kantorovich distance for PDEs: the coupling method. Preprint, 2019. arXiv:1903.11349Google Scholar
Judovič, V. I., Non-stationary flows of an ideal incompressible fluid. Ž. Vyčisl. Mat i Mat. Fiz. 3(1963), 1032–1066.Google Scholar
Loeper, G., Uniqueness of the solution to the Vlasov-Poisson system with bounded density. J. Math. Pures Appl. 86(2006), 68–79. https://doi.org/10.1016/j.matpur.2006.01.005CrossRefGoogle Scholar
Majda, A. J. and Bertozzi, A. L., Vorticity and incompressible flow. Cambridge Texts in Applied Mathematics, 27, Cambridge University Press, Cambridge, 2002.Google Scholar
Masmoudi, N., Remarks about the inviscid limit of the Navier-Stokes system. Comm. Math. Phys. 270(2007), 777–788. https://doi.org/10.1007/s00220-006-0171-5CrossRefGoogle Scholar
Seis, C., A quantitative theory for the continuity equation. Ann. Inst. H. Poincaré Anal. Non Linéaire 34(2017), 1837–1850. https://doi.org/10.1016/j.anihpc.2017.01.0001CrossRefGoogle Scholar
Seis, C., Optimal stability estimates for continuity equations. Proc. Roy. Soc. Edinburgh Sect. A 148(2018), 1279–1296. https://doi.org/10.1017/S0308210518000173CrossRefGoogle Scholar
Villani, C., Topics in optimal transportation. Graduate Studies in Mathematics, 58, American Mathematical Society, Providence, RI, 2003. https://doi.org/10.1090/gsm/058Google Scholar