Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T06:56:28.663Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on the Grothendieck Group of Subspaces of Rational Functions and Shokurov's Cartier b-divisors

Published online by Cambridge University Press:  20 November 2018

Kiumars Kaveh  and
A. G. Khovanskii
Kiumars Kaveh
Affiliation:
Department of Mathematics, University of Pittsburgh, Pittsburgh, PA, USA e-mail: [email protected]
A. G. Khovanskii
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON and Moscow Independent University, Institute for Systems Analysis, Russian Academy of Sciences e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a previous paper the authors developed an intersection theory for subspaces of rational functions on an algebraic variety 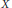$X$ over 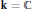$\mathbf{k}\,=\,\mathbb{C}$. In this short note, we first extend this intersection theory to an arbitrary algebraically closed ground field 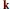$\mathbf{k}$. Secondly we give an isomorphism between the group of Cartier $b$-divisors on the birational class of 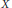$X$ and the Grothendieck group of the semigroup of subspaces of rational functions on 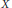$X$. The constructed isomorphism moreover preserves the intersection numbers. This provides an alternative point of view on Cartier $b$-divisors and their intersection theory.

Keywords

14C2014Exxintersection numberCartier divisorCartier b-divisorGrothendieck group
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 3 , 01 September 2014 , pp. 562 - 572
Copyright
Copyright © Canadian Mathematical Society 2014

References

[Fulton98] Fulton, W., Intersection theory. Second ed. Ergebnisse der Mathematik und ihrer Grenzgebiete, 3, Folge, A Series of Modern Surveys in Mathematics, 2, Springer-Verlag, Berlin, 1998.Google Scholar
[Hartshorne77] Hartshorne, R., Algebraic geometry. Graduate Texts in Mathematics, 52, Springer-Verlag, New York-Heidelberg, 1977.Google Scholar
[Iskovskikh03] Iskovskikh, V. A., b-divisors and Shokurov functional algebras. (Russian) Tr. Mat. Inst. Steklova 240 (2003), Biratsion. Geom. Linein. Sist. Konechno Porozhdennye Algebry, 8–20; translation in Proc. Steklov Inst. Math. 2003, no. 1 (240), 4–15.Google Scholar
[K-K10] Kaveh, K. and Khovanskii, A. G., Mixed volume and an extension of intersection theory of divisors. Mosc. Math. J. 10 (2010), no. 2, 343–375, 479.Google Scholar
[K-K12] Kaveh, K. and Khovanskii, A. G., Newton-Okounkov bodies, semigroups of integral points, graded algebras and intersection theory. Ann. of Math. 176 (2012), no. 2, 925–978. http://dx.doi.org/10.4007/annals.2012.176.2.5 Google Scholar
[L04] Lazarsfeld, R., Positivity in algebraic geometry. I. Classical setting: line bundles and linear series. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3, Folge, A Series of Modern Surveys in Mathematics, 48, Springer-Verlag, Berlin, 2004.Google Scholar
[M74] Manin, Yu. I., Cubic forms: algebra, geometry, arithmetic. North-Holland Mathematical Library, 4, North-Holland Publishing Co., Amsterdam-London; American Elsevier Publishing Co., New York, 1974.Google Scholar
[S-Z60] Samuel, P. and Zariski, O., Commutative algebra. Vol. II. Reprint of the 1960 ed., Graduate Texts in Mathematics, 29, Springer, New York, 1976.Google Scholar
[S03] Shokurov, V. V., Prelimiting flips. Tr. Mat. Inst. Steklova 240 (2003), Biratsion. Geom. Linein. Sist. Konechno Porozhdennye Algebry, 82–219; translation in Proc. Steklov Inst. Math. 2003, no. 1 (240), 75–213.Google Scholar