Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-22T20:36:37.004Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Quaternionic Hyperbolic Ideal Triangle Groups

Published online by Cambridge University Press:  20 November 2018

Wensheng Cao  and
Xiaolin Huang
Wensheng Cao
Affiliation:
School of Mathematics and Computational Science, Wuyi University, Jiangmen, Guangdong 529020, P.R. China e-mail: [email protected] e-mail: [email protected]
Xiaolin Huang
Affiliation:
School of Mathematics and Computational Science, Wuyi University, Jiangmen, Guangdong 529020, P.R. China e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, the quaternionic hyperbolic ideal triangle groups are parametrized by a real one-parameter family 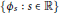$\{{{\phi }_{s}}\,:\,s\,\in \,\mathbb{R}\}$ . The indexing parameter s is the tangent of the quaternionic angular invariant of a triple of points in 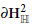$\partial \mathbf{H}_{\mathbb{H}}^{2}$ forming this ideal triangle. We show that if 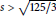$s>\sqrt{125/3},$ then 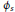${{\phi }_{S}}$ is not a discrete embedding, and if 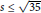$s\,\le \,\sqrt{3\text{5}}$ , then 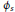${{\phi }_{S}}$ is a discrete embedding.

Keywords

20F6722E4030F40quaternionic inversionideal triangle groupquaternionic Cartan angular invariant
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 2 , 01 June 2016 , pp. 244 - 257
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Apanasov, B. N. and Kim, I., Cartan angular invariant and deformations of rank 1 symmetric spaces. Sbornik: Mathematics 198(2007), no. 2,147-169. http://dx.doi.org/10.4213/sm1112 Google Scholar
[2] Cao, W. S., Congruence classes of points in quaternionic hyperbolic space. Geom. Dedicata. 2015, doi:10.1007/sl0711-015-0099-zGoogle Scholar
[3] Cao, W. S. and Gongopadhyay, K., Algebraic characterization of isometries of the complex and the quaternionic hyperbolic planes. Geom. Dedicata. 157(2012), 23–39. http://dx.doi.org/10.1007/s10711-011-9599-7 Google Scholar
[4] Chen, S. S. and Greenberg, L., Hyperbolic spaces.In: Contributions to analysis. A collection of papers dedicated to LipmanBers. Academic Press, New York, 1974, pp. 49–87.Google Scholar
[5] Goldman, W. M., Complex hyperbolic geometry. Oxford Math. Monographs, The Clarendon Press Oxford University Press, New York, 1999.Google Scholar
[6] Goldman, W. M. and Parker, J. R., Complex hyperbolic ideal triangle groups.J. Reine Agnew. Math. 425(1992), 71–86.Google Scholar
[7] Goldman, W. M., Kapovich, M., and Leeb, B., Complex hyperbolic surfaces homotopy equivalent to a Riemann surface. Comm. Anal. Geom. 9(2001), 61–95.Google Scholar
[8] Kim, I. and Parker, J. R., Geometry of quaternionic hyperbolic manifolds. Math. Proc. Camb. Phil. Soc. 135(2003), 291–320. http://dx.doi.org/10.1017/S030500410300687X Google Scholar
[9] Maskit, B., Kleinian groups. Berlin-Heidelberg -New York, 1988.Google Scholar
[10] Mostow, G. D., On a remarkable class of polyhedra in complex hyperbolic space. Pacific. J. Math. 86(1980), 171–276. http://dx.doi.org/10.2140/pjm.1980.86.171 Google Scholar
[11] Parker, J. R., Complex hyperbolic lattices, discrete groups and geometric structures.Contemporary Mathematics, 501, American Mathematical Society, 2009, 1–42.Google Scholar
[12] Parker, J. R. and Platis, I. D., Complex hyperbolic quasi-Fuchsian groups. Geometry of Riemann Surfaces, London Mathematical Society Lecture Notes. 368 (2010), 309–355.Google Scholar
[13] Schwartz, R. E., Ideal triangle groups, dented tori, and numerical analysis. Ann. of Math. 153(2001), no. 2, 533–598. http://dx.doi.org/10.2307/2661362 Google Scholar
[14] Schwartz, R. E., Complex hyperbolic triangle groups. Proceedings of the International Congress of Mathematicians (2002) Vol. 1: Invited Lectures, 339–350.Google Scholar
[15] Schwartz, R. E. ” A better proof of the Goldman-Parker conjecture. Geom. Topol. 9(2005), 1539–1601. http://dx.doi.org/10.2140/gt.2005.9.1539 Google Scholar
[16] Thurston, W., The geometry and dynamics of surface diffeomorphisms.Bull. Amer. Math. Soc. Vol. 19., Oct. 1988. Notes, 1978.http://dx.doi.org/10.1090/S0273-0979-1988-15685-6 Google Scholar