Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-14T12:28:26.754Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on Pointwise Convergence on the Choquet Boundary

Published online by Cambridge University Press:  20 November 2018

Marvin W. Grossman
Marvin W. Grossman*
Affiliation:
Rutgers, The State University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [6] J. Rainwater obtained the following theorem.

Theorem. Let N be a normed linear space, {xn} a bounded sequence of elements in N and X ∊ N. 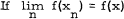for each extreme point f of the unit ball of N✶, then {xn} converges weakly to x.

Now let X be a compact Hausdorff space and H a linear subspace of C(X) (all real-valued continuous functions on X ) which separates the points of X and contains the constant functions. If x∊X, then MX(H) denotes the set of positive linear functionals μ on C(X) such that μ(h) = h(x) for all h in H.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 10 , Issue 1 , April 1967 , pp. 109 - 113
Copyright
Copyright © Canadian Mathematical Society 1967

Footnotes

1

This research was supported in part by NSF Grant GP 4413.

References

1. Bauer, H., Silovscher Rand und Dirichletsches Problem. Ann. Inst. Fourie. (Grenoble) 11 (1966), pages 89-136.CrossRefGoogle Scholar
2. Bishop, E. and de Leeuw, K., The representation of linear functionals by measures on sets of extreme points. Ann. Inst. Fourie. (Grenoble) 9 (1955), pages 305-331.CrossRefGoogle Scholar
3. Day, M. M., Normed Linear Spaces. Springer-Verlag, Berlin (1955).Google Scholar
4. Phelps, R. R., Lectures on Choquet's Theorem. D. Van Nostrand, Princeton (1966).Google Scholar
5. Pták, V., A combinatorial lemma on the existence of convex means and its applications to weak compactness. Proc. of Symposia in Pure Mathematics. Vol. 7, Convexity, Amer, Math. Soc. (1966), pages 211-219.Google Scholar
6. Rainwater, J., Weak convergence of bounded sequences. Proc. Amer. Math. Soc. 6 (1966), page 999.Google Scholar