Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-24T02:41:40.044Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Planarity Stratification of Hurwitz Spaces

Published online by Cambridge University Press:  20 November 2018

Jared Ongaro  and
Boris Shapiro
Jared Ongaro
Affiliation:
Department of Mathematics, Stockholm University, S-10691, Stockholm, Sweden e-mail: [email protected] [email protected]
Boris Shapiro
Affiliation:
Department of Mathematics, Stockholm University, S-10691, Stockholm, Sweden e-mail: [email protected] [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

One can easily show that any meromorphic function on a complex closed Riemann surface can be represented as a composition of a birational map of this surface to 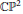$\mathbb{C}{{\mathbb{P}}^{2}}$ and a projection of the image curve froman appropriate point 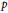$p\in \mathbb{C}{{\mathbb{P}}^{2}}$ to the pencil of lines through $p$ . We introduce a natural stratification of Hurwitz spaces according to the minimal degree of a plane curve such that a given meromorphic function can be represented in the above way and calculate the dimensions of these strata. We observe that they are closely related to a family of Severi varieties studied earlier by J. Harris, Z. Ran, and I. Tyomkin.

Keywords

14H5014H05Hurwitz spacesmeromorphic functionsSeveri varieties
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 3 , 01 September 2015 , pp. 596 - 609
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Aluffi, P., Two characteristic numbers for smooth plane curves of any degree. Trans. Amer. Math. Soc. 329(1992), no. 1,73–96. http://dx.doi.org/10.1090/S0002-9947-1992-1041042-5 Google Scholar
[2] Arbarello, E., Cornalba, M., Griffiths, P. A., and J. Harris, Geometry of algebraic curves. Vol. I. Grundlehren der MathematischenWissenschaften, 267, Springer-Verlag, New York, 1985.Google Scholar
[3] Bertrand, B., Brugalle, E., and Mikhalkin, G., Genus 0 characteristic numbers of the tropical protective plane. Compos.Math. 150(2014), no. 1, 46–104. http://dx.doi.Org/10.1112/S0010437X13007409 Google Scholar
[4] Burman, Yu. and Lvovski, S., On projections of smooth and nodal curves. arxiv:1311.1904Google Scholar
[5] Clebsch, A., XurThéorie der Riemann'schenFlàchen. Math. Ann. 6(1873), no. 2, 216–230. http://dx.doi.org/10.1007/BF01443193 Google Scholar
[6] Deopurkar, A. and Patel, A., The Picard rank conjecture for the Hurwitz spaces ofdegre e up to five. 9(2015), no. 2, 459–492. http://dx.doi.Org/10.2140/ant.2015.9.459 Google Scholar
[7] Ekedahl, T., Lando, S., Shapiro, M., and Vainshtein, A., Hurwitz numbers and intersections on moduli spaces of curves. Invent. Math. 146(2001), no. 2, 297–327. http://dx.doi.Org/10.1 OO7/sOO222O100164 Google Scholar
[8] Goulden, I. P., Jackson, D. M., and Vakil, R., A short proof of the Xg-conjecture without Gromov-Witten theory: Hurwitz theory and the moduli of curves. J. Reine Angew. Math. 637(2009), 175–191.Google Scholar
[9] Harris, J., On the Severi problem, Invent. Math. 84 (1986), no. 3, 445–461. http://dx.doi.org/10.1007/BF01388741 Google Scholar
[10] Harris, J. and Morrison, I., Moduli of curves. Graduate Texts in Mathematics, 187, Springer, New York, 1998.Google Scholar
[11] Hartshorne, R., Algebraic geometry. Graduate Texts in Mathematics, 52, Springer-Verlag, New York-Heidelberg, 1977.Google Scholar
[12] Hazewinkel, M. and Martin, C., A short elementary proof of Grothendieck's theorem on algebraic vector bundles over the projective line. J. Pur. Appl. Algebra 25(1982), no. 2, 207–211. http://dx.doi.Org/10.101 6/0022-4049(82)90037-8 Google Scholar
[13] Hurwitz, A., ÙberRiemann'scheFlàchen mit gegebenenVerzweigungspunkten. Math. Ann. 39(1891), no. 1, 1–60. http://dx.doi.org/10.1007/BF011 99469 Google Scholar
[14] Kleiman, S. L. and Schende, V. V., On the Gôttschethreshold. Clay Math. Proa, 18. In: A celebration of algebraic geometry, American Mathematical Society, Providence, RI, 2013, pp. 429-449.Google Scholar
[15] Maroni, A., Le série linearispecialisulle curve trigonali. Ann. Mat. Pura Appl. (4) 25(1946), 343–354.Google Scholar
[16] Miranda, R., Linear systems of plane curves. Notices Amer. Math.Soc. 46(1999), no. 2,192–201.Google Scholar
[17] Ohbuchi, A., On some numerica relations of d-gonal linear systems. J. Math. Tokushima Univ. 31(1997), 7–10.Google Scholar
[18] Patel, A. P., The geometry of Hurwitz space. PhD thesis, Harvard University, ProquestLLC, Ann Arbor, MI, 2013.Google Scholar
[19] Ran, Z., Families of plane curves and their limits: Enriques’ conjecture and beyond. An Mathn. 130(1989), no. 1, 121–157. http://dx.doi.Org/10.2307/1 971478 Google Scholar
[20] Severi, F., VorlesungentiberalgebraischeGéométrie. Teubner-Verlag, 1921.Google Scholar
[21] Tyomkin, I., On Severi varieties on Hirzebruch surfaces. Int. Math. Res. Not. IMRN 2007, no. 23, Art. ID rnmlO9.Google Scholar
[22] Vakil, R., Twelve points on the projective line, branched covers, and rational elliptic fibrations. Math. Ann. 320(2001), no. 1, 33–54. http://dx.doi.Org/10.1007/PL00004469 Google Scholar
[23] Vakil, R., The characteristic numbers of quartic plane curves. Canad. J. Math. 51(1999), no. 5, 1089–1120. http://dx.doi.org/10.4153/CJM-1999-048-1 Google Scholar
[24] Zeuten, H. G., AlmindeligeEgenskabervedsystemer of plane Kurver. KongeligeDanske VidenskabernesSelskabsSkrifter-NaturvidenskabeligogMathematisk 10(1873), 287–393.Google Scholar