Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T02:28:55.226Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Mal′cevian Varieties

Published online by Cambridge University Press:  20 November 2018

Ahmad Shafaat
Ahmad Shafaat*
Affiliation:
Dept. of Math., Laval University, Quebec, P.Q. Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By a homomorphic relation over an algebra A we mean a subalgebra of A × A. A variety [1[ 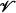of algebras will be called Mal′cevian [2[ if the identities of include two identities of the form f (x, y, y)=x, f(x, x, y)=y. In [3[ many examples and interesting properties of Mal′cevian varieties have been quoted or proved. In [4[ it is noted that every reflexive homomorphic relation over an algebra of a Mal′cevian variety is a congruence. The purpose of this short note is to observe that the property of Mal′cevian varieties noted in [1] is in fact characteristic of such varieties.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 17 , Issue 4 , 01 December 1974 , pp. 609
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Cohn, P.M., Universal Algebra, Harper and Row (1965).Google Scholar
2. MaFcev, A.I., On the general theory of algebraic systems, Mat. Sbornik N.S., 35 (1954), 3-20.Google Scholar
3. Lambek, J., Goursaf s theorem and the Zassenhaus lemma, Canad. J. Math. 10 (1957), 45-56.Google Scholar
4. Findlay, G.D., Reflexive homomorphic relations, Canad. Math. Bull. 3(2) 1960, 131-132.Google Scholar
5. Isidore Fleischer, , A note on subdirect products, Acta Math. Acad. Sci. Hungar., 6 (1955), 463-465.Google Scholar