Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-11T11:16:38.717Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Homological Dimensions of Artinian Local Cohomology Modules

Published online by Cambridge University Press:  20 November 2018

Kamal Bahmanpour
Kamal Bahmanpour*
Affiliation:
Department of Mathematics, Ardabil branch, Islamic Azad University, P.O. Box 5614633167, Ardabil, Iran e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 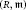$\left( R,\,m \right)$ be a non-zero commutative Noetherian local ring (with identity) and let $M$ be a non-zero finitely generated $R$-module. In this paper for any 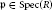$\mathfrak{p}\,\in \,\text{Spec}\left( R \right)$ we show that

1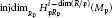

$$\text{injdi}{{\text{m}}_{{{R}_{\mathfrak{p}}}}}\,H_{\mathfrak{p}{{R}_{\mathfrak{p}}}}^{i-\dim\left( {R}/{\mathfrak{p}}\; \right)}\left( {{M}_{\mathfrak{p}}} \right)$$
and 1
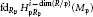$$\text{f}{{\text{d}}_{{{R}_{\mathfrak{p}}}}}H_{\mathfrak{p}}^{i-\dim\left( {R}/{\mathfrak{p}}\; \right)}\left( {{M}_{\mathfrak{p}}} \right)$$

are bounded from above by 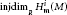$\text{injdi}{{\text{m}}_{R}}\,H_{\text{m}}^{i}\left( M \right)$ and 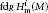$\text{f}{{\text{d}}_{R}}\,H_{\text{m}}^{i}\left( M \right)$ respectively, for all integers 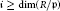$i\,\ge \,\dim\left( {R}/{\mathfrak{p}}\; \right)$.

Keywords

13D45cofinite modulesflat dimensioninjective dimensionKrull dimensionlocal cohomology
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 3 , 01 September 2013 , pp. 491 - 499
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Bahmanpour, K. and Naghipour, R., Cofiniteness of local cohomology modules for ideals of small dimension. J. Algebra 321 (2009), no. 7, 1997–2011. http://dx.doi.org/10.1016/j.jalgebra.2008.12.020 Google Scholar
[2] Brodmann, M. P. and Sharp, R. Y., Local cohomology: an algebraic introduction with geometric applications. Cambridge Studies in Advanced Mathematics, 60, Cambridge University Press, Cambridge, 1998.Google Scholar
[3] Delfino, D. and Marley, T., Cofinite modules and local cohomology. J. Pure and Appl. Algebra 121 (1997), no. 1, 45–52. http://dx.doi.org/10.1016/S0022-4049(9600044-8 Google Scholar
[4] Hartshorne, R., Local cohomology. A seminar given by A. Grothendieck. Lecture Notes in Mathematics, 41, Springer-Verlag, Berlin-New York, 1961).Google Scholar
[5] Hartshorne, R., Affine duality and cofiniteness. Invent. Math. 9(1969/1970), 145–164. http://dx.doi.org/10.1007/BF01404554 Google Scholar
[6] Matsumura, H., Commutative ring theory. Cambridge Studies in Advanced Mathematics, 8, Cambridge University Press, Cambridge, 1986).Google Scholar
[7] Melkersson, L., Modules cofinite with respect to an ideal. Algebra J. 285 (2005), no. 2, 649–668. http://dx.doi.org/10.1016/j.jalgebra.2004.08.037 Google Scholar
[8] Schenzel, P., Proregular sequences, local cohomology, and completion. Math. Scand. 92 (2003), no. 2, 161–180.Google Scholar
[9] Yoshida, K.-I., Cofiniteness of local cohomology modules for ideals of dimension one. Nagoya Math. J. 147 (1997), 179–191.Google Scholar