This note proves another special case of a conjecture of U. Oberst. Oberst considered [1], for any small category 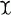, the X abelian category 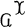of abelian group-valued functors on , and the X functor Colim: 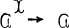which takes each diagram to its colimit. The question is, when is Colim exact? For its relationships, see [1], It is a sufficient condition that each component of is upward filtered. Oberst conjectured that it is also necessary, and proved this under some conditions. He mentioned particularly the case that 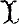is a monoid, i.e. a category with one object. We shall verify the conjecture in that case.