Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T16:39:40.997Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Asymptotic Normal Structure and Close-to-Normal Structure

Published online by Cambridge University Press:  20 November 2018

Kok-Keong Tan
Kok-Keong Tan*
Affiliation:
Department of Mathematics Statistics and Computing Science, Dalhousie University Halifax, Nova Scotia Canada B3H 4H8
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A closed convex subset X of a Banach space E is said to have (i) asymptotic normal structure if for each bounded closed convex subset C of X containing more than one point and for each sequence 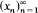in C satisfying ‖xn − xn + 1‖ → 0 as n → ∞, there is a point x ∈ C such that 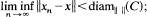; (ii) close-to-normal structure if for each bounded closed convex subset C of X containing more than one point, there is a point x ∈ C such that ‖x − y‖ < diam‖ ‖(C) for all y ∈ C While asymptotic normal structure and close-to-normal structure are both implied by normal structure, they are not related. The example that a reflexive Banach space which has asymptotic normal structure but not close-to normal structure provides us a non-empty weakly compact convex set which does not have close-to-normal structure. This answers an open question posed by Wong in [9] and hence also provides us a Kannan map defined on a weakly compact convex set which does not have a fixed point.

Keywords

46B2047H10Asymptotic normal structureclose-to-normal structurenormal structurenonexpansive mappingKannan mapfixed point
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 25 , Issue 3 , 01 September 1982 , pp. 339 - 343
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Alspach, D., A fixed point free nonexpansive map, Proc. Amer. Math. Soc. 82 (1981) 423-424.Google Scholar
2. Baillon, J.-B. and Schöneberg, R., Asymptotic normal structure and fixed points of nonexpansive mappings, Proc. Amer. Math. Soc. 81(1981) 257-264.Google Scholar
3. Brodskii, M. S. and Milman, D. P., On the centre of a convex set, Dokl. Akad. Nauk. SSSR 59 (1948), pp. 837-840, MR9 #448.Google Scholar
4. Kirk, W. A., A fixed point theorem for mappings which do not increase distance, Amer. Math. Monthl. 72 (1968), pp. 1004-1006.Google Scholar
5. Kirk, W. A., Fixed point theory for nonexpansive mappings, preprint.Google Scholar
6. Routledge, N. A., A result in Hilbert space, Quart. J. Math. 3 (1952), pp. 12-18.Google Scholar
7. Tan, K. K., A short proof of a theorem of Routledge, submitted.Google Scholar
8. Wong, C. S., Close-to-normal structure and its applications, J. Functiona. Analysi. 16 (1974), pp. 353-358.Google Scholar
9. Wong, C. S., On Kannan maps, Proc. Amer. Math. Soc. 47 (1975), pp. 105-111.Google Scholar
10. Wong, C. S., Fixed points and characterizations of certain maps, Pacifi. J. Math. 54 (1974), pp. 305-312.Google Scholar