Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-15T06:12:31.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on an Application of the δ-Function in the Representation of Solutions of Algebraic Equations

Published online by Cambridge University Press:  20 November 2018

J. B. Sabat
J. B. Sabat*
Affiliation:
Loyola of Montreal
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The “function” δ(x - xo) is known as the Dirac Delta function and may be defined as zero everywhere except at xo, where it is infinite in such a way that

1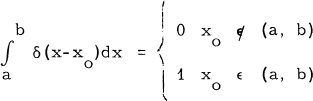

having property that for every continuous function φ(x) on (a, b)

2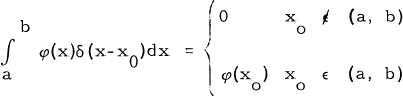

It is well known [2] δ(x-xo) can be approximated as a limit of a sequence of piecewise continuous functions, and there is an abundance of such sequences.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 10 , Issue 5 , December 1967 , pp. 735 - 738
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Friedman, B., Principles and techniques of applied mathematics (Wiley, 1956) p. 136.Google Scholar
2. Stakgold, I., Boundary value problems of mathematical physic. (Vol. 1), Macmiilan, 1967.Google Scholar