Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-13T11:54:54.696Z Has data issue: false hasContentIssue false
  • English
  • Français

A Norm Inequality for Linear Transformations

Published online by Cambridge University Press:  20 November 2018

B.N. Moyls  and
N.A. Khan
B.N. Moyls
Affiliation:
University of British Columbia
N.A. Khan
Affiliation:
Muslim University, Aligarh, India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1949 Ky Fan [1] proved the following result: Let λ1…λn be the eigenvalues of an Hermitian operator H on an n-dimensional vector space Vn. If x1, …, xq is an orthonormal set in V1, and q is a positive integer such n that 1 ≤ q ≤ n, then

1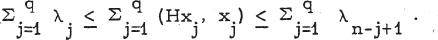

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 4 , Issue 3 , September 1961 , pp. 239 - 242
Copyright
Copyright © Canadian Mathematical Society 1961

References

1. Fan, K., On a theorem of Weyl concerning eigenvalues of linear transformations I, Proc. N. Acad. Sci. (U. S. A. ), 35 (1949), 652-655.Google Scholar