Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-16T16:25:38.226Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonvanishing of Central Values of L-functions of Newforms in S2(Γ0(dp2)) Twisted by Quadratic Characters

Published online by Cambridge University Press:  20 November 2018

Samuel Le Fourn
Samuel Le Fourn*
Affiliation:
ENS de Lyon, Lyon, France. [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that for 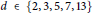$d\in \left\{ 2,3,5,7,13 \right\}$ and 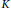$K$ a quadratic (or rational) field of discriminant 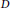$D$ and Dirichlet character 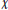$\chi $, if a prime 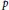$p$ is large enough compared to 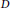$D$, there is a newform 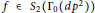$f\in {{S}_{2}}({{\Gamma }_{0}}(d{{p}^{2}}))$ with sign $(+1)$ with respect to the Atkin–Lehner involution 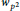${{w}_{{{p}^{2}}}}$ such that 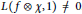$L(f\otimes \chi ,1)\ne 0$. This result is obtained through an estimate of a weighted sum of twists of $L$-functions that generalises a result of Ellenberg. It relies on the approximate functional equation for the $L$-functions 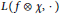$L(f\otimes \chi ,\cdot )$ and a Petersson trace formula restricted to Atkin–Lehner eigenspaces. An application of this nonvanishing theorem will be given in terms of existence of rank zero quotients of some twisted jacobians, which generalises a result of Darmon and Merel.

Keywords

14J1511F67nonvanishing of L-functions of modular formsPetersson trace formularank zero quotients of Jacobians
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 2 , 01 June 2017 , pp. 329 - 349
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Akbary, A., Non-vanishing ojmodular L-functions with large level. PhD Thesis, University of Toronto, 1997. http://www.cs.uleth.ca/∼akbary/publications.html Google Scholar
[2] Atkin, A. and Lehner, J., Hecke operators on T0(m). Math. Ann. 185(1970), 134–160. http://dx.doi.org/1 0.1007/BF01359701 Google Scholar
[3] Bump, D., Automorphic forms and representations. Cambridge Studies in Advanced Mathematics, 55, Cambridge University Press, Cambridge, 1997. http://dx.doi.org/10.1017/CBO9780511609572 Google Scholar
[4] Chen, I., On Relations between facobians of certain modular curves. J. Algebra 231(2000), no. 1, 414–448. http://dx.doi.org/10.1006/jabr.2000.8375 Google Scholar
[5] Darmon, H. and Merel, L., Winding quotients and some variants ofFermat's Last Theorem. J. Reine Angew. Math. 490(1997), 81–100. Google Scholar
[6] de Smit, B. and Edixhoven, B., Sur un résultat d'Imin Chen. Mat. Res. Lett. 7(2000), no. 2-3, 147–153. http://dx.doi.org/10.4310/MRL.2000.v7.n2.a1 Google Scholar
[7] Elkies, N., On Elliptic K-curves. In: Modular curves and Abelian varieties, Prog. Math., 224, Birkhâuser, Basel, 2004, pp. 81–91.Google Scholar
[8] Ellenberg, J., Galois representations attached to Q-curves and the generalized Fermât equationA4+B2= Cp. Amer. J. Math. 126(2004), 763–787. http://dx.doi.org/10.1353/ajm.2004.0027 Google Scholar
[9] Ellenberg, J., On the error term in Duke's estimate for the average special value of L-functions. Canad. Math. Bull. 48(2005), 535–546. http://dx.doi.org/1 0.41 53/CMB-2005-049-8 Google Scholar
[10] Guo, J., On the positivity of the central critical values of automorphic L-f unctions for GL(2). Duke Math. J. 83(1996, no. 1, 157–190. http://dx.doi.org/10.1215/S0012-7094-96-08307-6 Google Scholar
[11] Hardy, G. and Wright, E., An introduction to the theory of numbers. Sixth éd., Oxford University Press, Oxford, 2008.Google Scholar
[12] Iwaniec, H. and Kowalski, E., Analytic number theory. American Mathematical Society Colloquium Publications, 53, American Mathematical Society, Providence, RI, 2004. http://dx.doi.org/10.1090/coll/053 Google Scholar
[13] Iwaniec, H. and Sarnak, P., The non-vanishing of central values of automorphic L-functions and Landau-Siegel zeros. Israel J. Math. 120(2000), 155–177. Google Scholar
[14] Kolyvagin, V. and Logach, D.ëv, Finiteness of the Shafarevich-Tate group and the group of rational points for some modular abelian varieties. Leningrad Math. J. 1(1990), 1229–1253. Google Scholar
[15] Le Fourn, S. , Points entiers et rationnels sur des courbes et variétés modulaires de dimension supérieure. Thèse, Université de Bordeaux, 2015. Google Scholar
[16] Le Fourn, S. , Surjectivity of Galois representations associated with quadratic Q-curves. Math. Ann. 365(2015), no. 1-2, 173–214. http://dx.doi.org/10.1007/s00208-015-1269-x Google Scholar
[17] Rankin, R., Modular forms and functions. Cambridge University Press, Cambridge, 1977. Google Scholar
[18] Watson, G., Treatise on the theory of Bessel functions. Cambridge Mathematical Library, 1922.Google Scholar