No CrossRef data available.
Published online by Cambridge University Press: 22 November 2024
We study the Abel-Jacobi image of the Ceresa cycle  $W_{k, e}-W_{k, e}^-$, where
$W_{k, e}-W_{k, e}^-$, where  $W_{k, e}$ is the image of the k-th symmetric product of a curve X with a base point e on its Jacobian variety. For certain Fermat quotient curves of genus g, we prove that for any choice of the base point and
$W_{k, e}$ is the image of the k-th symmetric product of a curve X with a base point e on its Jacobian variety. For certain Fermat quotient curves of genus g, we prove that for any choice of the base point and 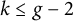 $k \leq g-2$, the Abel-Jacobi image of the Ceresa cycle is non-torsion. In particular, these cycles are non-torsion modulo rational equivalence.
$k \leq g-2$, the Abel-Jacobi image of the Ceresa cycle is non-torsion. In particular, these cycles are non-torsion modulo rational equivalence.