Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-16T16:08:38.729Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-splitting in Kirchberg's Ideal-related KK-Theory

Published online by Cambridge University Press:  20 November 2018

Søren Eilers ,
Gunnar Restorff  and
Efren Ruiz
Søren Eilers
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Copenhagen, Denmarke-mail: [email protected]
Gunnar Restorff
Affiliation:
Faculty of Science and Technology, University of Faroe Islands, Tórshavn, Faroe Islandse-mail: [email protected]
Efren Ruiz
Affiliation:
Department of Mathematics, University of Hawaii Hilo, Hilo, Hawaii, U.S.A.e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A. Bonkat obtained a universal coefficient theorem in the setting of Kirchberg's ideal-related 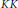$KK$-theory in the fundamental case of a 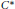${{C}^{*}}$-algebra with one specified ideal. The universal coefficient sequence was shown to split, unnaturally, under certain conditions. Employing certain $K$-theoretical information derivable from the given operator algebras using a method introduced here, we shall demonstrate that Bonkat's 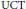$\text{UCT}$ does not split in general. Related methods lead to information on the complexity of the $K$-theory which must be used to classify $*$-isomorphisms for purely infinite 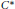${{C}^{*}}$-algebras with one non-trivial ideal.

Keywords

46L35KK-theoryUCT
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 1 , 01 March 2011 , pp. 68 - 81
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Bonkat, A., Bivariante K-Theorie für Kategorien projektiver Systeme von C*-Algebren. Ph.D. thesis, Westfälische Wilhelms-Universität, 2002. http://wwwmath1.uni-muenster.de/sfb/about/publ/heft319.ps.Google Scholar
[2] Cuntz, J., A class of C*-algebras and topological Markov chains. II. Reducible chains and the Ext-functor for C*-algebras. Invent. Math. 63(1981), no. 1, 25–40. doi=10.1007/BF01389192Google Scholar
[3] Dădărlat, M. and Eilers, S., Compressing coefficients while preserving ideals in the K-theory for C*-algebras. K-Theory 14(1998), no. 3, 281–304. doi=10.1023/A:1007744626135Google Scholar
[4] Dădărlat, M. and Loring, T., A universal multicoefficient theorem for the Kasparov groups. Duke Math. J. 84(1996), no. 2, 355–377. doi=10.1215/S0012-7094-96-08412-4Google Scholar
[5] Eilers, S., Loring, T., and Pedersen, G., Stability of anticommutation relations: an application of noncommutative CW complexes. J. Reine Angew. Math. 499(1998), 101–143.Google Scholar
[6] Eilers, S. and Restorff, G., On Rørdam's classification of certain C*-algebras with one nontrivial ideal. In: Operator algebras: The Abel symposium 2004, Abel Symp., 1, Springer, Berlin, 2006, pp. 87–96.Google Scholar
[7] Higson, N., A characterization of KK-theory. Pacific J. Math. 126(1987), 253–276.Google Scholar
[8] Kasparov, G. G., The operator K-functor and extensions of C*-algebras. (Russian) Izv. Akad. Nauk SSSR Ser. Mat. 44(1980), no. 3, 571–636, 719.Google Scholar
[9] Kirchberg, E., Das nicht-kommutative Michael-Auswahlprinzip und die Klassifikation nicht-einfacher Algebren. In: C*-algebras (Münster, 1999), Springer, Berlin, 2000, 92–141.Google Scholar
[10] Kirchberg, E. and Phillips, N. C., Embedding of exact C*-algebras in the Cuntz algebra . J. Reine Angew. Math. 525(2000), 17–53. doi=10.1515/crll.2000.065Google Scholar
[11] Meyer, R. and Nest, R., C*-Algebras over topological spaces: Filtrated K-theory. arXiv:0810.0096v2[math.OA]Google Scholar
[12] Restorff, G., Classification of Cuntz-Krieger algebras up to stable isomorphism. J. Reine Angew. Math. 598(2006), 185–210. doi=10.1515/CRELLE.2006.074Google Scholar
[13] Restorff, G., Classification of non-simple C*-algebras. Ph. D. thesis, Department of Mathematical Sciences, University of Copenhagen, 2008. http://www.math.ku.dk/»restorff/papers/thesis.pdfGoogle Scholar
[14] Restorff, G. and Ruiz, E., On Rørdam's classification of certain C*-algebras with one nontrivial ideal, II. Math. Scand. 101(2007), 280–292.Google Scholar
[15] Rørdam, M., Classification of extensions of certain C*-algebras by their six term exact sequences in K-theory. Math. Ann. 308(1997), no. 1, 93–117. doi=10.1007/s002080050067Google Scholar
[16] Rosenberg, J. and Schochet, C., The Künneth theorem and the universal coefficient theorem for Kasparov's generalized K-functor. Duke Math. J. 55(1987), no. 2, 431–474. doi=10.1215/S0012-7094-87-05524-4Google Scholar
[17] Schochet, C., The UCT, the Milnor sequence, and a canonical decomposition of the Kasparov groups. K-Theory 10(1996), no. 1, 49–72. doi=10.1007/BF00534888Google Scholar
[18] Schochet, C., Correction to: “The UCT, the Milnor sequence, and a canonical decomposition of the Kasparov groups”. K-Theory 14(1998), no. 2, 197–199. doi=10.1023/A:1007736102864Google Scholar
[19] Schochet, C., The fine structure of the Kasparov groups. II. Topologizing the UCT. J. Funct. Anal. 194(2002), no. 2, 263–287. doi=10.1006/jfan.2002.3949Google Scholar