Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T04:19:34.432Z Has data issue: false hasContentIssue false
  • English
  • Français

A New Method for High-Degree Spline Interpolation: Proof of Continuity for Piecewise Polynomials

Part of: Approximations and expansions Numerical approximation and computational geometry Numerical methods in Fourier analysis

Published online by Cambridge University Press:  09 December 2019

A. Pepin ,
S. S. Beauchemin ,
S. Léger  and
N. Beaudoin
A. Pepin
Affiliation:
Département de mathématiques et de statistique, Pavillon Rémi-Rossignol, Université de Moncton, 18 avenue Antonine-Maillet, Moncton, Canada, E1A 3E9 Email: [email protected]@umoncton.ca
S. S. Beauchemin
Affiliation:
Department of Computer Science, University of Western Ontario, Middlesex College 28C, London, Canada, N6A 5B7 Email: [email protected]
S. Léger
Affiliation:
Département de mathématiques et de statistique, Pavillon Rémi-Rossignol, Université de Moncton, 18 avenue Antonine-Maillet, Moncton, Canada, E1A 3E9 Email: [email protected]@umoncton.ca
N. Beaudoin
Affiliation:
Département de physique et d’astronomie, Pavillon Rémi-Rossignol, Université de Moncton, 18 avenue Antonine-Maillet, Moncton, Canada, E1A 3E9 Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Effective and accurate high-degree spline interpolation is still a challenging task in today’s applications. Higher degree spline interpolation is not so commonly used, because it requires the knowledge of higher order derivatives at the nodes of a function on a given mesh.

In this article, our goal is to demonstrate the continuity of the piecewise polynomials and their derivatives at the connecting points, obtained with a method initially developed by Beaudoin (1998, 2003) and Beauchemin (2003). This new method, involving the discrete Fourier transform (DFT/FFT), leads to higher degree spline interpolation for equally spaced data on an interval 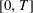$[0,T]$. To do this, we analyze the singularities that may occur when solving the system of equations that enables the construction of splines of any degree. We also note an important difference between the odd-degree splines and even-degree splines. These results prove that Beaudoin and Beauchemin’s method leads to spline interpolation of any degree and that this new method could eventually be used to improve the accuracy of spline interpolation in traditional problems.

Keywords

splinecontinuityFFTDFTdiscrete Fourier transformnumerical derivative

MSC classification

Primary: 41A15: Spline approximation
Secondary: 65D05: Interpolation 65D07: Splines 65T50: Discrete and fast Fourier transforms
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 3 , September 2020 , pp. 655 - 669
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

We would like to acknowledge the financial support of the Natural Sciences and Engineering Research Council of Canada (NSERC), the New Brunswick Innovation Foundation (NBIF), the Université de Moncton and Assumption Life.

References

Ahlberg, J. H., Nilson, E. N., and Walsh, J. L., The theory of splines and their applications. Academic Press, New York-London, 1967.Google Scholar
Beauchemin, N. and Beauchemin, S. S., A new numerical Fourier transform in d-dimensions. IEEE Trans. Signal Process. 51(2003), 1422–1430. https://doi.org/10.1109/TSP.2003.810285Google Scholar
Beaudoin, N., Tutorial/Article didactique: A high-accuracy mathematical and numerical method for Fourier transform, integral, derivatives, and polynomial splines of any order. Canadian J. Phys. 76(1998), 659–677.Google Scholar
Cahill, N., et al. , Fibonacci determinants. College Math. J. 33(2002).Google Scholar
De Boor, C., A practical guide to splines. Applied Mathematical Sciences, 27, Springer-Verlag, New York-Berlin, 1978.10.1007/978-1-4612-6333-3CrossRefGoogle Scholar
Foata, D., Eulerian polynomials: from Euler’s time to the present. In: The legacy of Alladi Ramakrishnan in the mathematical sciences. Springer, New York, 2010, pp. 253–273. https://doi.org/10.1007/978-1-4419-6263-8_15CrossRefGoogle Scholar
Froeyen, M. and Hellemans, L., Improved algorithm for the discrete Fourier transform. Review of Scientific Instruments 56(1985), 2325–2327.CrossRefGoogle Scholar
Graham, R. L., Knuth, D. E., and Patashnik, O., Concrete mathematics. A foundation for computer science. Second ed., Addison-Wesley Publishing Company, Reading, MA, 1994.Google Scholar
Kyrala, A., Applied functions of a complex variable. Wiley-Interscience, New York-London-Sydney, 1972.Google Scholar
Merca, M., A note on the determinant of a Toeplitz-Hessenberg matrix. Spec. Matrices 2(2014), 10–16.Google Scholar
Mäkinen, S., New algorithm for the calculation of the Fourier transform of discrete signals. Review of Scientific Instruments 53(1982), 627–630.10.1063/1.1137022CrossRefGoogle Scholar
Petersen, K. T., Eulerian numbers. Birkhäuser Advanced Texts: Basel Textbooks, Birkhäuser/Springer, New York, 2015.10.1007/978-1-4939-3091-3CrossRefGoogle Scholar
Savage, C. D. and Mirkó, V., The s-Eulerian polynomials have only real roots. Trans. Amer. Math. Soc. 367(2015), 1441–1466. https://doi.org/10.1090/S0002-9947-2014-06256-9CrossRefGoogle Scholar
Schütte, J., New fast Fourier transform algorithm for linear system analysis applied in molecular beam relaxation spectroscopy. Review of Scientific Instruments 52(1981), 400–404.10.1063/1.1136592CrossRefGoogle Scholar
Sorella, S. and Ghosh, S. K., Improved method for the discrete fast Fourier transform. Review of Scientific Instruments 55(1984), 1348–1352.10.1063/1.1137938CrossRefGoogle Scholar