Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-09T13:12:19.097Z Has data issue: false hasContentIssue false
  • English
  • Français

A New Inversion and Representation Theory for the Laplace Transform

Published online by Cambridge University Press:  20 November 2018

H. P. Heinig
H. P. Heinig*
Affiliation:
McMaster University, Hamilton, Ontario and University of Toronto
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If

1.1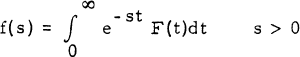

and

1.2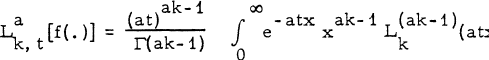

a ≥ 0, k=1, 2, 3, …; where 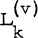is the Laguerre polynomial of order v, defined by

then we shall show that under certain conditions

1.3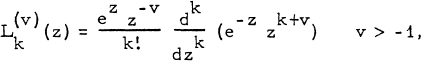

Following the inversion theory, two representation theorems are given. The proofs of these theorems follow easily along the lines of Widder [4, Ch. VII] and are therefore omitted.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 9 , Issue 4 , October 1966 , pp. 447 - 455
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Erdélyi, A., The inversion of the Laplace transform. Math. Mag., vol. 24, (1950–51), pp. 1-7.Google Scholar
2. Erdélyi, A. et al, Higher transcendental functions, vol.2, N.Y. (1953).Google Scholar
3. Hirschman, I.I. Jr., A new representation and inversion theory for the Laplace integral. Duke Math. J.,15 (2), (1948).Google Scholar
4. Widder, D.V., The Laplace transform. Princeton, (1946).Google Scholar