Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T06:22:33.887Z Has data issue: false hasContentIssue false
  • English
  • Français

A new complemented subspace for the Lorentz sequence spaces, with an application to its lattice of closed ideals

Part of: Normed linear spaces and Banach spaces; Banach lattices Linear spaces and algebras of operators

Published online by Cambridge University Press:  02 August 2021

Ben Wallis
Ben Wallis*
Affiliation:
Division of Math/Science/Business, Kishwaukee College, Malta, IL60150, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

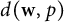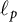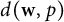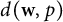We show that every Lorentz sequence space $d(\textbf {w},p)$ admits a 1-complemented subspace Y distinct from $\ell _p$ and containing no isomorph of $d(\textbf {w},p)$ . In the general case, this is only the second nontrivial complemented subspace in $d(\textbf {w},p)$ yet known. We also give an explicit representation of Y in the special case 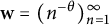$\textbf {w}=(n^{-\theta })_{n=1}^\infty $ (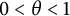 $0<\theta <1$ ) as the 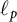$\ell _p$ -sum of finite-dimensional copies of 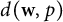$d(\textbf {w},p)$ . As an application, we find a sixth distinct element in the lattice of closed ideals of 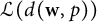$\mathcal {L}(d(\textbf {w},p))$ , of which only five were previously known in the general case.

Keywords

Lorentz sequence spacescomplemented subspaceslattice of closed ideals

MSC classification

Primary: 46B20: Geometry and structure of normed linear spaces
Secondary: 46B45: Banach sequence spaces 47L20: Operator ideals
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 3 , September 2022 , pp. 759 - 769
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altshuler, Z., Casazza, P. G., and Lin, B.-L., On symmetric basic sequences in Lorentz sequence spaces . Israel J. Math. 15(1973), no. 2, 140–155.CrossRefGoogle Scholar
Casazza, P. G. and Lin, B.-L., On symmetric basic sequences in Lorentz sequence spaces II . Israel J. Math. 17(1974), 191–218.10.1007/BF02882238CrossRefGoogle Scholar
Heinrich, S., Ultraproducts in Banach space theory . J. Reine Angew. Math. 313(1980), 72–104.Google Scholar
Johnson, W. B. and Lindenstrauss, J., Basic concepts in the geometry of Banach spaces . In: Johnson, W. B. and Lindenstrauss, J. (eds.), Handbook of the geometry of Banach spaces, Vol. 1, Elsevier, Amsterdam, 2001, pp. 1–84.CrossRefGoogle Scholar
Kadec, M. I. and Pełczyński, A., Bases, lacunary sequences and complemented subspaces in the spaces Lp . Studia Math. 21(1962), 161–176.10.4064/sm-21-2-161-176CrossRefGoogle Scholar
Kaminska, A., Popov, A. I., Spinu, E., Tcaciuc, A., and Troitsky, V. G., Norm closed operator ideals in Lorentz sequence spaces . J. Math. Anal. Appl. 389(2012), no. 1, 247–260.CrossRefGoogle Scholar
Laustsen, N. J., Loy, R. J., and Read, C. J., The lattice of closed ideals in the Banach algebra of operators on certain Banach spaces . J. Funct. Anal. 214(2004), 106–131.CrossRefGoogle Scholar
Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces I, sequence spaces, Springer, Berlin, 1977.Google Scholar
Wallis, B., Closed ideals of operators acting on some families of sequence spaces . Banach J. Math. Anal. 14(2020), no. 1, 98–115.CrossRefGoogle Scholar