Let G be a group and ρ and σ two irreducible unitary representations of G in complex Hilbert spaces and assume that dimp ρ= n < ∞. D. Poguntke [2] proved that 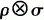is a sum of at most n2 irreducible subrepresentations. The case when dim a is also finite he attributed to R. Howe.

We shall prove analogous results for arbitrary finite-dimensional representations, not necessarily unitary. Thus let F be an algebraically closed field of characteristic 0. We shall use the language of modules and we postulate that allour modules are finite-dimensional as F-vector spaces. The field F itself will be considered as a trivial G-module.