Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-22T05:39:57.014Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiplicative Structure of the Ring K(S(T*ℝP2n+1))

Published online by Cambridge University Press:  20 November 2018

M. A. Bousaidi
M. A. Bousaidi*
Affiliation:
Mathematics Department Mohamed V University B.P: 1014, Rabat Morocco
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We calculate the additive and multiplicative structure of the ring 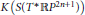$K\left( S\left( {{T}^{*}}\mathbb{R}{{P}^{2n+1}} \right) \right)$ using the eta invariant.

Keywords

19L6419K5655C35
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 1 , 01 March 2000 , pp. 37 - 46
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Gilkey, P. B., Invariance theory, the heat equation and the Atiyah-Singer Index theorem. Publish or Perish, Wilmington, Delaware, 1984.Google Scholar
[2] Gilkey, P. B., The eta invariant and K-theory of odd dimensional spherical space forms. Invent. Math. 76 (1984), 421–453.Google Scholar
[3] Gilkey, P. B., The eta invariant for even dimensional Pin c manifolds. Adv. in. Math. (3) 58 (1985), 243–284.Google Scholar
[4] Gilkey, P. B., The Geometry of Spherical Space Form Groups. World Scientific Press (Singapore) Series in Pure Math. 7(1989).Google Scholar
[5] Karoubi, M., K-theory, an introduction. Springer-Verlag, 1978.Google Scholar
[6] Snaith, V., The K-theory of the cotangent sphere bundle of RPn . Canada. Math. Bull. (1) 29(1986).Google Scholar