Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-24T01:30:30.386Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple Solutions for Nonlinear Periodic Problems

Published online by Cambridge University Press:  20 November 2018

Sophia Th. Kyritsi  and
Nikolaos S. Papageorgiou
Sophia Th. Kyritsi
Affiliation:
Department of Mathematics, Hellenic Naval Academy, Piraeus 18539, Greece e-mail: [email protected]
Nikolaos S. Papageorgiou
Affiliation:
National Technical University, Department of Mathematics, Zografou Campus, Athens 15780, Greece e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider a nonlinear periodic problem driven by a nonlinear nonhomogeneous differential operator and a Carathéodory reaction term 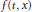$f\left( t,\,x \right)$ that exhibits a 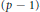$\left( p\,-\,1 \right)$-superlinear growth in 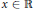$x\,\in \,\mathbb{R}$ near 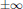$\pm \infty $ and near zero. A special case of the differential operator is the scalar 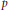$p$-Laplacian. Using a combination of variational methods based on the critical point theory with Morse theory (critical groups), we show that the problem has three nontrivial solutions, two of which have constant sign (one positive, the other negative).

Keywords

34B1534B1834C2558E05C-conditionmountain pass theoremcritical groupsstrong deformation retractcontractible spacehomotopy invariance
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 2 , 01 June 2013 , pp. 366 - 377
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Aizicovici, S., Papageorgiou, N. S., and Staicu, V., Periodic solutions for second order differential inclusions with the p-Laplacian. J. Math. Anal. Appl. 322(2006), no. 2, 913–929. http://dx.doi.org/10.1016/j.jmaa.2005.09.077 Google Scholar
[2] Ben-Naoum, A. K. and De Coster, C., On the existence and multiplicity of positive solutions of the p-Laplacian separated boundary value problem. Differential Integral Equations 10(1997), no. 6, 1093–1112. Google Scholar
[3] Chang, K.-C., Infinite dimensional Morse theory and multiple solution problems. Progress in Nonlinear Differential Equations and their Applications, 6, Birkhäuser Boston, Boston, MA, 1993.Google Scholar
[4] Costa, D. G. and Magalhães, C. A., Existence results for perturbations of the p-Laplacian. Nonlinear Anal. 24(1995), no. 3, 409–418. http://dx.doi.org/10.1016/0362-546X(94)E0046-J Google Scholar
[5] De Coster, C., Pairs of positive solutions for one-dimensional p-Laplacian. Nonlinear Anal. 23(1994), no. 5, 669–681. http://dx.doi.org/10.1016/0362-546X(94)90245-3 Google Scholar
[6] del Pino, M. A., Manásevich, R., and Murua, A. E., Existence and multiplicity of solutions with prescribed period for a second order quasilinear ODE. Nonlinear Anal. 18(1992), no. 1, 79–92. http://dx.doi.org/10.1016/0362-546X(92)90048-J Google Scholar
[7] Fei, G., On periodic solutions of superquadratic Hamiltonian systems. Electron. J. Differential Equations 2002, no. 8, 12 pp.Google Scholar
[8] Gasiński, L. and Papageorgiou, N. S., On the existence of multiple periodic solutions for equations driven by the p-Laplacian and a nonsmooth potential. Proc. Edinb. Math. Soc. 46(2003), no. 1, 229–249. Google Scholar
[9] Granas, A. and Dugundji, J., Fixed point theory. Springer Monographs in Mathematics, Springer-Verlag, New York, 2003.Google Scholar
[10] Mańasevich, R., Njoku, F. I., and Zanolin, F., Positive solutions for the one-dimensional p-Laplacian. Differential Integral Equations 8(1995), no. 1, 213–222. Google Scholar
[11] Montenegro, M., Strong maximum principles for supersolutions of quasilinear elliptic equations. Nonlinear Anal. 37(1999), no. 4, 431–448. http://dx.doi.org/10.1016/S0362-546X(98)00057-1 Google Scholar
[12] Njoku, F. I. and Zanolin, F., Positive solutions for two-point BVPs: existence and multiplicity results. Nonlinear Anal. 13(1989), no. 11, 1329–1338. http://dx.doi.org/10.1016/0362-546X(89)90016-3 Google Scholar
[13] Papageorgiou, N. S. and S. Th. Kyritsi-Yiallourou, Handbook of applied analysis. Advances in Mechanics and Mathematics, 19, Springer, New York, 2009.Google Scholar
[14] Papageorgiou, E. H. and Papageorgiou, N. S., Two nontrivial solutions for quasilinear periodic equations. Proc. Amer. Math. Soc. 132(2004), no. 2, 429–434. http://dx.doi.org/10.1090/S0002-9939-03-07076-X Google Scholar
[15] Papageorgiou, N. S. and Papalini, F., Pairs of positive solutions for the periodic scalar p-Laplacian. J. Fixed Point Theory Appl. 5(2009), no. 1, 157–184. http://dx.doi.org/10.1007/s11784-008-0061-x Google Scholar
[16] Yang, X., Multiple periodic solutions of a class of p-Laplacian. J. Math. Anal. Appl. 314(2006), no. 1, 17–29. Google Scholar