No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
We shall consider scalar transport phenomena in which the mass distribution of a large number of interacting mass particles varies as a result of multiple coalescence mechanisms. Four models will be considered; all the particles are of the same kind in the first three. In the first model an integer n (n≥2) is given and the coalescence mechanism is such that under suitable conditions n particles of masses xl…, xn combine to form one particle of mass 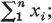 we refer to this as the n/1 transport.
we refer to this as the n/1 transport.