Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T23:57:28.065Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple Lattice Tilings in Euclidean Spaces

Part of: Designs and configurations Real and complex geometry Discrete geometry

Published online by Cambridge University Press:  16 November 2018

Qi Yang  and
Chuanming Zong
Qi Yang
Affiliation:
School of Mathematical Sciences, Peking University, Beijing 100871, China
Chuanming Zong
Affiliation:
Center for Applied Mathematics, Tianjin University, Tianjin 300072, China Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1885, Fedorov discovered that a convex domain can form a lattice tiling of the Euclidean plane if and only if it is a parallelogram or a centrally symmetric hexagon. This paper proves the following results. Except for parallelograms and centrally symmetric hexagons, there are no other convex domains that can form two-, three- or four-fold lattice tilings in the Euclidean plane. However, there are both octagons and decagons that can form five-fold lattice tilings. Whenever 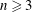$n\geqslant 3$, there are non-parallelohedral polytopes that can form five-fold lattice tilings in the $n$-dimensional Euclidean space.

MSC classification

Primary: 52C20: Tilings in $2$ dimensions
Secondary: 52C22: Tilings in $n$ dimensions 05B45: Tessellation and tiling problems 52C17: Packing and covering in $n$ dimensions 51M20: Polyhedra and polytopes; regular figures, division of spaces
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 4 , December 2019 , pp. 923 - 929
Copyright
© Canadian Mathematical Society 2018 

Footnotes

This work was supported by 973 Program 2013CB834201. Author C. Z. is the corresponding author.

References

Aleksandrov, A. D., On completion of a space by polyhedra . Vestnik Leningrad Univ. Ser. Mat. Fiz. Him. 9(1954), 33–43.Google Scholar
Blunden, W. J., Multiple covering of the plane by circles . Mathematika 4(1957), 7–16. http://doi.org/10.1112/S0025579300001042 Google Scholar
Blunden, W. J., Multiple packing of circles in the plane . J. London Math. Soc. 38(1963), 176–182. http://doi.org/10.1112/jlms/s1-38.1.176 Google Scholar
Bolle, U., On the density of multiple packings and coverings of convex discs . Studia Sci. Math. Hungar. 24(1989), 119–126.Google Scholar
Bolle, U., On multiple tiles in E 2 . In: Intuitive geometry, Colloq. Math. Soc. J. Bolyai, 63. North-Holland, Amsterdam, 1994.Google Scholar
Cohn, M. J., Multiple lattice covering of space . Proc. London Math. Soc. 32(1976), 117–132. http://doi.org/10.1112/plms/s3-32.1.117 Google Scholar
Delone, B. N., Sur la partition regulière de l’espace à 4 dimensions I, II . Izv. Akad. Nauk SSSR, Ser. VII (1929), 79–110, 147–164.Google Scholar
Dumir, V. C. and Hans-Gill, R. J., Lattice double packings in the plane . Indian J. Pure Appl. Math. 3(1972), 481–487.Google Scholar
Dutour Sikirić, M., Garber, A., Schürmann, A., and Waldmann, C., The complete classification of five-dimensional Dirichlet–Voronoi polyhedra of translational lattices . Acta Crystallogr. A72(2016), 673–683. http://doi.org/10.1107/s2053273316011682 Google Scholar
Engel, P., On the symmetry classification of the four-dimensional parallelohedra . Z. Krist. 200(1992), 199–213. http://doi.org/10.1524/zkri.1992.200.3-4.199 Google Scholar
Fedorov, E. S., Elements of the study of figures . Zap. Mineral. Imper. S. Petersburgskogo Obšč. 21(1885), 1–279. Načala učeniya o figurah. (Russian) (Elements of the study of figures.) Izdat. Akad. Nauk SSSR, Moscow, 1953.Google Scholar
Fejes Tóth, G., Multiple lattice packings of symmetric convex domains in the plane . J. London Math. Soc. 29(1984), 556–561. http://doi.org/10.1112/jlms/s2-29.3.556 Google Scholar
Furtwängler, P., Über Gitter konstanter Dichte . Monatsh. Math. Phys. 43(1936), 281–288. http://doi.org/10.1007/BF01707607 Google Scholar
Gravin, N., Robins, S., and Shiryaev, D., Translational tilings by a polytope, with multiplicity . Combinatorica 32(2012), 629–649. http://doi.org/10.1007/s00493-012-2860-3 Google Scholar
Gravin, N., Kolountzakis, M. N., Robins, S., and Shiryaev, D., Structure results for multiple tilings in 3D . Discrete Comput. Geom. 50(2013), 1033–1050. http://doi.org/10.1007/s00454-013-9548-3 Google Scholar
Groemer, H., Multiple packings and coverings . Studia Sci. Math. Hungar. 21(1986), 189–200.Google Scholar
Gruber, P. M. and Lekkerkerker, C. G., Geometry of numbers . Second ed., North-Holland Mathematical Library, 37. North-Holland, Amsterdam, 1987.Google Scholar
Hajós, G., Über einfache und mehrfache Bedeckung des n-dimensionalen Raumes mit einem Würfelgitter . Math. Z. 47(1941), 427–467. http://doi.org/10.1007/BF01180974 Google Scholar
Kolountzakis, M. N., On the structure of multiple translational tilings by polygonal regions . Discrete Comput. Geom. 23(2000), 537–553. http://doi.org/10.1007/s004540010014 Google Scholar
Lagarias, J. C. and Zong, C., Mysteries in packing regular tetrahedra . Notices Amer. Math. Soc. 59(2012), 1540–1549. http://doi.org/10.1090/noti918 Google Scholar
Mann, C., McLoud-Mann, J., and Von Derau, D., Convex pentagons that admit i-block transitive tilings . Geom. Dedicata 194(2018), 141–167. http://doi.org/10.1007/s10711-017-0270-9 Google Scholar
McMullen, P., Convex bodies which tiles space by translation . Mathematika 27(1980), 113–121. http://doi.org/10.1112/S0025579300010007 Google Scholar
Minkowski, H., Allgemeine Lehrsätze über konvexen Polyeder . Nachr. K. Ges. Wiss. Göttingen, Math.-Phys. KL. (1897), 198–219.Google Scholar
Rao, M., Exhaustive search of convex pentagons which tile the plane. arxiv:1708.00274 Google Scholar
Reinhardt, K., Über die Zerlegung der Ebene in Polygone. Dissertation, Universität Frankfurt am Main, 1918.Google Scholar
Robinson, R. M., Multiple tilings of n-dimensional space by unit cubes . Math. Z. 166(1979), 225–264. http://doi.org/10.1007/BF01214145 Google Scholar
Štogrin, M. I., Regular Dirichlet–Voronoi partitions for the second triclinic group. (in Russian) In: Proceedings of the Steklov Institute of Mathematics, 123. American Mathematical Society, Providence, RI, 1975.Google Scholar
Venkov, B. A., On a class of Euclidean polytopes . Vestnik Leningrad Univ. Ser. Mat. Fiz. Him. 9(1954), 11–31.Google Scholar
Voronoi, G. F., Nouvelles applications des parammètres continus à la théorie des formes quadratiques. Deuxième Mémoire. Recherches sur les paralléloèdres primitifs . J. reine angew. Math. 134(1908), 198–287. http://doi.org/10.1515/crll.1908.134.198 Google Scholar
Zong, C., What is known about unit cubes . Bull. Amer. Math. Soc. 42(2005), 181–211. http://doi.org/10.1090/S0273-0979-05-01050-5 Google Scholar
Zong, C., The cube: a window to convex and discrete geometry . Cambridge Tracts in Mathematics, 168. Cambridge University Press, Cambridge, 2006. http://doi.org/10.1017/CBO9780511543173 Google Scholar
Zong, C., Packing, covering and tiling in two-dimensional spaces . Expo. Math. 32(2014), 297–364. http://doi.org/10.1016/j.exmath.2013.12.002 Google Scholar