Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-22T06:17:12.581Z Has data issue: false hasContentIssue false
  • English
  • Français

More Problems Connected with Convexity

Published online by Cambridge University Press:  20 November 2018

Z.A. Melzak
Z.A. Melzak*
Affiliation:
University of British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This is a continuation of the author's article [3], and it contains further problems connected with the theory of convex sets in En. To the list of general references in [3] may be added the recent book [2] on convex polyhedra.

1) Let A and B be two convex bodies in E2 and let a packing P = {B1, B2, …} be an infinite sequence of homothetic images of B sucn that:

  1. a) each Bn is a subset of A,

  2. b) no two of them share interior points,

  3. c) Area (A) =

The existence of such packings is guaranteed by Vitali's Theorem. Let D(X) be the diameter of the set X and put .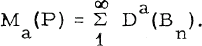

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 11 , Issue 3 , August 1968 , pp. 489 - 494
Copyright
Copyright © Canadian Mathematical Society 1968

References

1. Floyd, E.E., Functions defined on a sphere. Proc. Amer. Math. Soc. 6 (1955) 957-959.Google Scholar
2. Gruenbaum, B. (et al), Convex polytopes. (Interscience, New York, 1967).Google Scholar
3. Melzak, Z. A., Problems connected with convexity. Canad. Math, Bull. 8 (1965) 565-573.Google Scholar