Hostname: page-component-f554764f5-nt87m Total loading time: 0 Render date: 2025-04-09T01:29:08.585Z Has data issue: false hasContentIssue false
  • English
  • Français

Moments of the free Jacobi process: A matrix approach

Part of: Probability theory on algebraic and topological structures Special matrices Selfadjoint operator algebras Combinatorics, graph theory, probability theory, statistics

Published online by Cambridge University Press:  10 March 2025

Nizar Demni  and
Tarek Hamdi Open the ORCID record for Tarek Hamdi [Opens in a new window]
Nizar Demni
Affiliation:
Department of Mathematics, New York University in Abu Dhabi, Saadiyat Island, P.O. Box 129188, Abu Dhabi, UAE e-mail: [email protected]
Tarek Hamdi*
Affiliation:
Department of Management Information Systems, College of Business and Economics, Qassim University, Buraydah, Saudi Arabia and Laboratoire d’Analyse Mathématiques et applications LR11ES11, Université de Tunis El-Manar, Tunis, Tunisia
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We compute the large size limit of the moment formula derived in [14] for the Hermitian Jacobi process at fixed time. Our computations rely on the polynomial division algorithm which allows to obtain cancellations similar to those obtained in [3, Lemma 3]. In particular, we identify the terms contributing to the limit and show they satisfy a double recurrence relation. We also determine explicitly some of them and revisit a special case relying on Carlitz summation identity for terminating 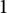$1$-balanced 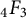${}_4F_3$ functions taken at unity.

Keywords

Hermitian Jacobi processfree Jacobi processMethod of momentshypergeometric functionsCarlitz summation formula

MSC classification

Primary: 15B52: Random matrices 33C80: Connections with groups and algebras, and related topics 46L54: Free probability and free operator algebras 60B20: Random matrices (probabilistic aspects; for algebraic aspects see ) 97K60: Distributions and stochastic processes
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 26
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abiodun, R. F. A., An application of Carlitz’s formula . J. Math. Anal. Appl. 70(1979), 114–119.Google Scholar
Bailey, W. N., Generalized hypergeometric series, Cambridge University Press, Cambridge, 1935.Google Scholar
Biane, P., Free Brownian motion, free stochastic calculus and random matrices, Fields Institute Communications, 12, American Mathematical Society, Providence, RI, 1997, pp. 1–19.Google Scholar
Capitaine, M. and Casalis, M., Asymptotic freeness by generalized moments for Gaussian and Wishart matrices. Application to beta random matrices . Indiana Univ. Math. J. 53(2004), no. 2, 397–431.Google Scholar
Carré, C., Deneufchatel, M., Luque, J. G., and Vivo, P., Asymptotics of Selberg-like integrals: The unitary case and Newton’s interpolation formula . J. Math. Phys. 51(2010), no. 12, 19.Google Scholar
Chu, W., Transformation formulae for terminating balanced 4F3-series and implications . Hacet. J. Math. Stat. 52(2023), no. 2, 391–397.Google Scholar
Collins, B., Product of random projections, Jacobi ensembles and universality problems arising from free probability . Probab. Theory Related Fields. 133(2005), no. 3, 315–344.Google Scholar
Dahlqvist, A., Integration formulas for Brownian motion on classical compact Lie groups . Ann. Inst. Henri Poincaré Probab. Stat. 53(2017), no. 4, 1971–1990.Google Scholar
Deleaval, L. and Demni, N., Moments of the Hermitian matrix Jacobi process . J. Theoret. Probab. 31(2018), no. 3, 1759–1778.Google Scholar
Demni, N., Free Jacobi process . J. Theor. Probab. 21(2008), 118–143.Google Scholar
Demni, N., $\beta$ -Jacobi processes . Adv. Pure Appl. Math. 1(2010), no. 3, 325–344.Google Scholar
Demni, N. and Hamdi, T., Summing free unitary Brownian motions with applications to quantum information . Lett. Math. Phys. 113(2023), no. 4, Paper No. 80, 39 pp.Google Scholar
Demni, N., Hamdi, T., and Hmidi, T., Spectral distribution of the free Jacobi process . Indiana Univ. Math. J. 61(2012), no. 3, 1351–1368.Google Scholar
Demni, N., Hamdi, T., and Souaissi, A., The Hermitian Jacobi process: a simplified formula for the moments and applications to optical fiber MIMO channels . Funct. Anal. Appl. 54(2020), no. 4, 257–271.Google Scholar
Doumerc, Y., Matrices aléatoires, processus stochastiques et groupes de réflexions. Ph.D. Thesis, Paul Sabatier University, 2005. Available at http://perso.math.univ-toulouse.fr/ledoux/doctoral-students/.Google Scholar
Forrester, P. J., Log-gases and random matrices, London Mathematical Society Monographs Series, 34, Princeton University Press, Princeton, NJ, 2010, xiv+791 pp.Google Scholar
Goulden, I. and Greene, C., A new tableau representation for supersymmetric Schur functions . J. Algebra. 170(1994), 687–703.Google Scholar
Graczyk, P. and Malecki, J., Strong solutions of non-colliding particle systems . Electron. J. Probab. 19(2014), no. 119, 1–21.Google Scholar
Hamdi, T., Spectral distribution of the free Jacobi process, revisited . Anal. PDE 11(2018), no. 8, 2137–2148.Google Scholar
Hamdi, T., Free mutual information for two projections . Complex Anal. Oper. Theory 12(2018), no. 7, 1697–1705 Google Scholar
Hiai, F. and Petz, D., The semicircle law, free random variables and entropy, Mathematical Surveys and Monographs, 77, American Mathematical Society, Providence, RI, 2000, x+376 pp.Google Scholar
Kesten, H., Symmetric random walks on groups . Trans. Amer. Math. Soc. 92(1959), 336–354.Google Scholar
Krattenthaler, C., Asymptotic analysis of a Selberg-type integral via hypergeometrics. e-print arXiv:1004.3941.Google Scholar
Lévy, T., Schur? Weyl duality and the heat kernel measure on the unitary group . Adv. Math. 218(2008), no. 2, 537–575.Google Scholar
McKay, B. D., The expected eigenvalue distribution of a large regular graph . Linear Algebra Appl. 40(1981), 203–216.Google Scholar
Merca, M., A generalisation of the symmetry between complete and elementary symmetric functions . Indian J. Pure Appl. Math. 45(2014), no. 1, 75–89.Google Scholar
Miller, A. R. and Paris, R. B., On a result related to transformations and summations of generalized hypergeometric series . Math. Commun. 17(2012), no. 1, 205–210.Google Scholar
Reiner, V., Non-crossing partitions for classical reflection groups . Discrete Math. 177(1997), 195–222.Google Scholar
Shapiro, L. W., A Catalan triangle . Discrete Math. 14(1976), no. 1, 83–90.Google Scholar
Trinh, H. D. and Trinh, K. D., Beta Jacobi ensembles and associated Jacobi polynomials . J. Stat. Phys. 185(2021), no. 1, Paper No. 4, 15 pp.Google Scholar
Vidunas, R., Degenerate Gauss hypergeometric functions . Kyushu J. Math. 61(2007), no. 1, 109–135.Google Scholar
Voit, M., Freezing limits for Calogero-Moser-Sutherland particle models . Stud. Appl. Math. 151(2023), no. 4, 1230–1281.Google Scholar
Zyczkowski, K., Penson, K. A., Nechita, I., and Collins, B., Generating random density matrices . J. Math. Phys. 52(2011), no. 6, 62201, 20 pp.Google Scholar