Published online by Cambridge University Press: 20 November 2018
The sequence to sequence quasi - Hausdorff transformations were defined by Hardy [1] 1 1. 19 p. 277 as follows. For a given sequence {μn} (n ≥ 0) of real or complex numbers, define the operator Δ by 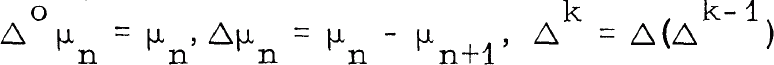 for k > l. {tm} (m ≥ 0) is called the sequence to sequence quasi-Hausdorff transform by means of {μn} (or, in short, the [QH, μn] transform) of {sn} (n ≥ 0) if if
for k > l. {tm} (m ≥ 0) is called the sequence to sequence quasi-Hausdorff transform by means of {μn} (or, in short, the [QH, μn] transform) of {sn} (n ≥ 0) if if 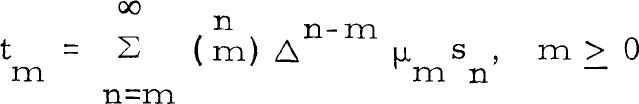 , provided that the sums on the right-hand side converge for all m ≥ 0. Ramanujan in [11] and [12] has defined the series to series quasi-Hausdorff transformation s and has proved necessary and sufficient conditions for the regularity of the two kinds of transformations.
, provided that the sums on the right-hand side converge for all m ≥ 0. Ramanujan in [11] and [12] has defined the series to series quasi-Hausdorff transformation s and has proved necessary and sufficient conditions for the regularity of the two kinds of transformations.